文章專區

純粹出於慣例，我們常常把0.05的「p值」視為研究結果具備統計顯著意義（statistically significant）的臨界標準。換句話說，當p值＜0.05，也就是結果純粹出於偶然的機率小於5％時，我們才說它具備統計顯著意義。由於研究人員比較有意閱讀具備統計顯著意義的「肯定」結果，而非不具備統計顯著意義的「否定」結果，這促使作者與期刊都爭相提出結果具備顯著意義的研究。研究人員和期刊為何對否定的研究結果不感興趣？

我們不完全清楚，不過倒可提出幾個合理的肇因。其一可能與我們的心理有關；對大多數人而言，否定的結果感覺起來有點乏味。「這兩種群類並無不同。」「這種治療方式不會改變結果。」「了解x對預測y沒有幫助。」讀這些句子時，我們會覺得自己沒學到跟周遭世界相關的有趣知識，反而又回到原點。

否定的結果可能還讓人想到執行技術性實驗的能力不足。卡爾任職於某家微生物實驗室時，常常沒辦法在瓊脂平皿上培養出他要研究的微生物大腸桿菌。這並非有趣的科學結果；只是顯示他在實驗室環境下完全無能而已。

第三種可能解釋是否定命題（negative propositions）沒有價值。不成立的假設隨口一說就有。隨機用字詞湊成的句子通常都不成立。「鬱金香會咬人。」「雪花會融掉鐵。」「大象就是鳥。」想在這片滿是不成立之陳述的海洋中找出成立之陳述，猶如想在充滿鬼扯的稻草堆裡找出一根具有意義的針。把這想成海戰棋（Battleship）這個老桌遊吧！棋盤格上大多數的空間都是開放的水域，因此沒打到對手的船艦就得知不了什麼資訊，不過一旦擊中對手的船艦，大量資訊到手，便可進一步習得更多資訊。

基於所有這些理由，否定的結果根本吸引不了大量的注意力。我們從未見過有人發表演說大談自己在實驗室裡做不成的研究、結果卻獲獎或成功謀得一職的例子。

雖然極少數科學家甘願犯下科學欺詐，以換取自己要的「p值」，但破壞科學過程之誠正性的灰色地帶依然很多。研究人員有時會嘗試不同的統計假設或檢驗方式，直到找出方法將自己的p值一點一點下修到具備統計顯著意義的臨界值0.05為止。這就是所謂的「p 值竄改」，屬於很嚴重的問題。或者，他們會修改自己的檢驗結果。某個臨床試驗一開始可能要測量使用某種新藥五年後對存活率的影響，不過，當研究人員發現毫無改變，他們可能會探勘資料，以找出用藥三年後對生活品質的明顯改善。

在分析自己蒐集的數據資料時，我們往往可以做各種選擇決定究竟要將什麼納入研究內容。舉例來說，假定我想研究選舉結果如何影響美國止痛藥的消費狀況。我可能會將選舉結果做成表格，蒐集服用止痛藥的調查報告，在找出過去以來止痛藥銷售量的數據資料。在此我有程度不等的自由度。我要檢視的選舉為何？美國總統選舉、美國參議員選舉、美國眾議會議員選舉、州長選舉、州參議員選舉、州眾議員選舉、市長選舉、市議會議員選舉等。我要調查男性或是女性的消費狀況，抑或兩者都調查？消費族群是年輕人、中年人、或是65歲以上的人、青少年，或者以上皆是？我要看的是民主黨候選人對上共和黨候選人的選舉效應，或是個人偏好的候選人對上非偏好的候選人的選舉效應？換句話說，我要不要對照止痛藥使用者的政治立場？還有，止痛藥的定義是什麼？阿斯匹靈（Aspirin）、安舒疼（Advil）、泰諾（Tylenol）、氫可酮（hydrocodone）、疼始康定（OxyContin）？我要比較單一地點選前選後的止痛藥消費狀況，還是只比較不同地點選後的結果？在我分析數據資料之前要做的決定極為龐雜。由於排列組合情況如此之多，很有可能最起碼有一個組合會呈現具備統計顯著意義的結果，即便選舉結果和止痛藥的使用情況根本沒有因果關係也無妨。

為了避免落入這樣的陷阱，研究人員在審視數據資料前就該明確做好這些所有選擇，接著再檢驗他們事先下定決心研究的假設。舉例來說，我可能決定檢驗已達法定選舉年紀的成年男女在個人偏好的州長候選人落選後，是否會服用更多止痛藥。或者，我可能要檢驗共和黨候選人取代民主黨候選人贏得美國眾議院議員選舉的選區裡，兒童用泰諾的銷量是否下滑。無論我選擇要檢視的對象為何，重點都是分析數據資料前就明白訂出。否則的話，只要我檢驗的假設夠多，一定會找到某些具備統計顯著意義的結果，即便真正的型樣不存在也無所謂。

不過，從研究人員的角度來看看吧。想像一下你才花了好幾月的時間蒐集龐大的數據資料集。你檢驗了自己的主要假設，也得到前景有望的研究結果，只不過它們不具備統計顯著意義。你明白這麼一來就沒辦法在知名的期刊發表這份研究，也許完全發表不了。你心想，可是這個假設的確成立，也許只是數據資料還不夠而已。於是你繼續蒐集數據資料直到你的「p值」降到0.05以下，然後你立刻就此打住以免數值浮動又高過那個臨界值。

也許你嘗試了其他幾個統計檢驗。由於數計資料已經快要具備統計顯著意義了，選對方法與檢驗，你就得以跨過「p值」＝0.05的關鍵門檻。想當然爾，稍做修改，你就會找出結果具備統計顯著意義的方法。

也許你的假設顯然只在男性身上成立，而本來有意義的型樣因為樣本當中加入女性卻消失了。你檢查了一下，瞧啊，只看男性的話，你就有具備統計顯著意義的結果了。你要怎麼辦？取消整個計畫，放棄已經投資的幾千美元，然後叫你指導的研究生再延6個月才畢業⋯⋯或乾脆報告男性的結果就好，然後投稿頂尖的期刊？在這些情況下，或許合理化後者的作法感覺起來很容易。「我確信真的有這個趨勢」，你可能會這麼跟自己說。「我一開始就考慮要刪除研究中的女性了。」

恭喜你。你剛剛竄改了研究的「p值」！

想像有1,000位誠正無欺的研究人員全都拒絕在任何情況下竄改「p值」。這些品行端正的學者們檢驗了1,000個攸關政治勝選與止痛劑使用情況之關係的假設，結果通通不成立。純粹出於偶然，這些假設中大概有50個達到「p值」＝0.05的等級，具備統計學上的真憑實據。50名幸運的研究人員提出他們的結果投稿期刊，順利通過審核獲得發表。其他950名研究人員裡只有一些人會大費周章地提出自己的否定研究結果，最後也只有少數人有辦法發表自己的否定研究結果。

當讀者審視文獻時，會看到50份研究顯示政治選舉結果和止痛藥的消費情況有關，也許還會看到幾個發現兩者不具關聯性的研究報告。他會合理認定政治對止痛藥的使用有重大影響，至於沒有成功的研究肯定只是量錯數量或找錯型樣。然而，事實卻恰恰相反，這兩者根本沒有關係，兩者出現關聯純粹是我們認為何種研究結果才有出版價值的人為現象。

此處根本的問題在於，論文能否獲得發表的機率與其提出之p值間並非毫無關係。因此，我們會迎頭碰上取樣偏誤的問題。發表的論文集合代表所有做過的實驗集合中的一個偏差樣本（biased sample）。具備統計顯著意義的結果在科學文獻裡比例過高，而不具統計顯著意義的結果卻比例過低。那些產出不具統計顯著意義結果的實驗數據資料最後都被丟進了科學家們的檔案櫃裡（現在或許被丟進電腦檔案系統裡）。有時候我們就稱這為檔案抽屜效應（file drawer effect）。

還記得古德哈特定律（Goodhart's Law）嗎？「當測量成為目標，它就不再是個好的測量標準」。某種程度上這就是p值的情況。由於p值低於0.05已經是論文發表的必要條件，所以p值便不再是具備統計說服力的有效測量標準。如果科學論文出版與否與p值無關，這些數值便依舊是檢測否定虛無假設的統計學證據說服力多高的有用標準。話說回來，既然期刊嚴重偏好p值低於0.05的論文，p值便不再符合最初的用意。

2005 年流行病學家約翰．伊奧尼迪斯（John Ioannidis）以聳動的標題「為什麼大部分出版的研究結果都是假的」（Why Most Published Research Findings Are False），著文概述檔案抽屜效應造成的後果。要解釋伊奧尼迪斯的論點，我們得先離題探討人稱「基本率謬誤」（base rate fallacy）的統計陷阱。

想像你是位醫師，正在治療某個擔心自己去緬因州釣魚時可能染上萊姆病（Lyme disease）的年輕人。回家後他人就一直不舒服，但目前還沒有出現跟萊姆病有關的輪狀紅疹特殊病徵。你覺得染病機會不大，但為了讓他安心，你答應檢測他血液中有無造成此病的細菌抗體。

讓你們兩人驚愕的是檢驗結果竟為陽性。檢測本身可稱準確，但並非精準無比。大概會出現5％的偽陽性。如此一來，你的病人染上萊姆病的機率為何？

許多人，包含許多醫師在內，會認為答案約為95％上下。這是不正確的。95％是指沒有萊姆病的人測出陰性的機率。你想知道的是有萊姆病之人測得陽性的機率。事實上由於萊姆病相當罕見，所以這個機率很低，在萊姆病盛行的地區每1,000個人大概也只有1人受到感染。想像一下你檢測10,000個人，你預期大約會有10個真陽性，同時還有約0.05×10,000＝500個偽陽性。每50個測出陽性的人當中，真正染病的不到1人。因此你可以預期自己的病人得到萊姆病的機率不到2％，即便測出陽性也一樣。

這種混淆，也就是以為病人有95％的機率染病，實際機率卻小於2％，這應該很常見的錯誤。這就是檢察官的謬誤，只不過老瓶換新酒而已。有時候我們會稱之為基本率謬誤，因為它涉及到解釋檢驗結果時卻忽略患病人口基本率的狀況。

回想一下檢察官的謬誤所用的表格：

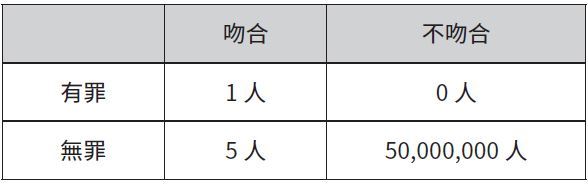
討論基本率謬誤時要用的類似表格，則如下所示：

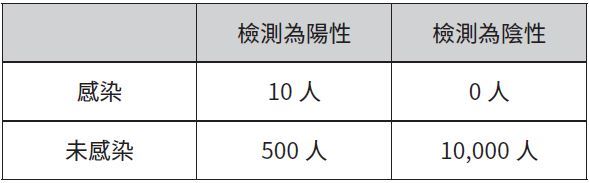
每一個例子的錯誤都一樣：比較的不是左邊欄位的機率，而是底部那一列的機率。

如果你檢測的是相當常見的病症，基本率謬誤就不是大問題。假定病人是來自美國中西部北邊的年輕白人女性，你為了治療她的胃疾，決定使用尿素呼氣試驗法（Urea Breath Test）檢測她有無胃幽門螺旋桿菌（Helicobacter pylori，簡稱幽門桿菌），也就是一種跟消化性潰瘍有關的病原體。此法跟萊姆病的抗體檢驗一樣，約有5％未受感染的人會測得陽性。假使你的病人測出陽性，她帶有幽門桿菌的機率為何？一樣是百分之一嗎？不對，比這要高多了，因為幽門桿菌是常見的病原體。美國約莫有20％的白人帶有幽門桿菌。現在想像一下你在10,000人身上檢測此病原體。你會發現大約2,000 例陽性，而剩下的8,000人當中大概有5％，即400人會測得偽陽性的結果。所以美國每6位幽門桿菌檢測結果為陽性的白人，大概就有5位真的帶有此病原體。解釋完基本率謬誤，讓我們回到伊奧尼迪斯身上。

他的論文「為什麼大部分出版的研究結果都是假的？」認為科學研究跟醫學檢驗的解釋方式有異曲同工之妙。他認為出版偏誤致使否定的研究結果大多沒有發表，而文獻內容幾乎都是肯定的研究結果。如果科學家們檢驗的是不太可能成立的假設，那絕大多數肯定的研究結果就是偽陽性，一如在沒有其他風險因子的情況下有無萊姆病的檢測結果幾乎都是偽陽性一樣。

我們說完了。那就是完整的論點。我們不太能質疑伊奧尼迪斯的數學。就他的模型來看，他的結論也正確。而且，他還有我們先前探討過的論文提供的實證支持，也就是證明許多優秀期刊發表的實驗無法被複製的那些論文，倘若那些肯定的實驗結果很多都是偽陽性，這便完全在我們的預料之中。

接著要談的是關於伊奧尼迪斯的假設前提，我們能提出的反駁。發表的研究結果若要多數為假，科學實驗就必須如罕見疾病般極不可能驗出真陽性。但科學不是那樣運作的，因為科學家們得以選擇自己要檢驗的假設。我們已經明白科學家深諳自己專業領域的獎勵結構，靠著發表引人興趣的研究內容最能累積獎勵，而且否定的研究結果是很難獲得發表。所以我們認為科學家會傾向檢驗雖未定論但比較可能成立的假設。這會讓我們偏向研究絕大多數之陽性結果皆為真陽性的幽門桿菌相關領域。由於伊奧尼迪斯對研究人員決定檢驗的那類假設認定有誤，不符現實，我們認為他過於悲觀。

當然，這都是理論上的推測而已。倘若我們想真的測量出版偏誤的問題多麼嚴重，我們就得知道：（1）檢驗過的假設實際為真的比例為何，還有（2）否定的研究結果獲得發表的比例為何。如果兩者比例皆高，就沒什麼好擔心的。假如兩者比例皆低，就有問題了。

我們已經闡述過科學家會傾向檢驗有可能成立的假設。可能性也許為10％、50％、或75％不等，但不會是1％或0.01％。至於否定的研究結果獲得發表的情況又如何呢？頻率多高？就跨科學領域整體而言，所有出版的研究中否定的結果約占15％。若屬生物醫學領域則為10％。社會心理學領域只有5％。問題在於我們無法從這些數據得知心理學家比較不可能發表否定的研究結果，還是他們選擇的實驗比較有可能產出肯定的研究結果。我們真正想知道的並不是所有發表的研究中否定的結果占比多高。我們想知道的是否定的研究結果獲得發表的比例為何。

書　名｜《數據的假象：數據識讀是深度偽造時代最重要的思辨素養，聰明決策不被操弄》
作　者｜卡爾‧ 伯格斯特姆、杰文‧ 威斯特（Carl T. Bergstrom, Jevin D. West）
譯　者｜穆思婕、沈聿德
出版社｜天下雜誌
出版日期｜ 2022 年6 月

數學、統計與科學都是理性、客觀、精確的代表，但也是資訊時代更容易操弄人心的騙術，而且更難被識破！

有圖有照片不一定有真相，數字表格簡單清楚其實更容易藏貓膩，大數據陷阱多多更容易扯大謊。

如何偵測科學鬼扯？如何識破數據資料不合邏輯的破綻？是現在深度偽造時代非常重要的自保能力。

兩位作者在華盛頓大學開設同名課程，受到極高的討論和迴響，他們運用統計與生物學領域的專精知識和經驗，以生動幽默的方式，拆解取樣偏誤與數據資料數位化混淆視聽的案例，檢視我們的生活多麼容易受到各類數據假象的影響。