文章專區

Take Home Message
► 品客洋芋片的特殊造型稱為「雙曲拋物面」，它是一種對外在壓力具有較高承受度的曲面，無論從哪一側擠壓，都比較不容易破碎。
► 直紋曲面是由一條直線在空間中連續變動所掃出的曲面，如果曲面由兩條不同的直線各自連續變動而掃出，就會被稱為雙直紋曲面。而雙曲拋物面上任一點都有兩條直線通過，幾何學家就稱這類曲面為「雙直紋曲面」，雙曲拋物面、平面、單葉雙曲面都是一種雙直紋曲面。
► 雙曲拋物面是一種簡單、容易建造的建築屋頂造型。優點是由材料重量所產生的力，可以由向上彎曲部分所產生的張力來拉住，不用在下方設置許多樑柱來支撐屋頂，而屋頂的重量也不像圓頂會對整個外牆都產生外推的力。

你有沒有過「花錢買空氣」的經驗呢？先別急著否認，其實我們每個人或多或少都曾做過這件事，那就是——買洋芋片。每當我們興沖沖地買了洋芋片回家，打開包裝卻發現裡面的份量只有三分之一後，那種失落感想必是大家的共同回憶之一。但消費者真的只是花錢買空氣的冤大頭嗎？其實洋芋片包裝裡的大量氮氣，除了可以防止洋芋片氧化之外，還有防止洋芋片碰撞後碎裂的功能。

不知道大家腦中有沒有想到另一種洋芋片，它被裝在圓柱形的筒子裡，形狀長得很特別——沒錯，就是品客（Pringles）洋芋片！但其實根據其原製造公司寶僑（Procter & Gamble, P&G）的說法，品客的馬鈴薯含量不到50％，而且具有「自然界找不到的特殊形狀」，只能算是加工後的脆片或餅乾，和一般由馬鈴薯切成薄片油炸而成的洋芋片不同。寶僑之所以希望品客被歸類為餅乾，並不是出自於他們對食物分類的職人堅持，而是希望這些洋芋片被賣到英國時，能夠免徵高達17.5％的洋芋片加值稅。

特殊「雙曲拋物面」 解決洋芋片易碎的問題

暫且不談稅金的問題，寶僑所謂「自然界找不到的特殊形狀」是什麼意思呢？品客洋芋片每一片的形狀都一模一樣，像是一個圓盤的東西兩端向上翹，南北兩端則向下凹（圖一），看起來蠻美觀的，不過這種形狀有什麼特殊之處嗎？

圖一：品客洋芋片的形狀被寶僑形容為「自然界找不到的特殊形狀」，
它像是一個圓盤的東西兩端向上翹，南北兩端則向下凹，這種造型有什麼特別之處？（123RF）

這就得從1950 年代說起。當時寶僑為了洋芋片易碎的問題傷透腦筋，他們找了美國有機化學家與食品儲存科學家包爾（Fredric John Baur）來解決這個問題。包爾想了兩個方法，一個是從洋芋片的形狀下手，另外則是設計堅固的包裝。由於包爾對油炸用油也很有研究，他認為把洋芋片炸成「雙曲拋物面」（hyperbolic paraboloid）的形狀可以讓洋芋片不易碎裂，而他也重新設計了圓筒型的包裝材料，進一步確保洋芋片受到撞擊時可分散衝擊力。

包爾的這兩個設計持續到今日，一直是品客的招牌特色呢！而寶僑為了把洋芋片做成雙曲拋物面的形狀並順利裝筒，更聘請了好幾位專家來設計各個環節，包括將馬鈴薯切成細粉、加料、重新塑形成圓盤狀、擺好油炸、最後疊好，因為這樣的設計，品客便不再是單純的洋芋片，而是調味過的「馬鈴薯脆片」囉。不過寶僑這樣大費周章，就只是為了把洋芋片弄成雙曲拋物面的形狀嗎？沒錯，當其他洋芋片都是「花錢買空氣」時，品客卻因為其特殊的幾何設計而能塞滿整罐，還被戲稱為最有良心、最實在的洋芋片呢。

為什麼雙曲拋物面能承受較大的壓力？

這個特別的「雙曲拋物面」究竟有什麼特點，為什麼包爾會選擇將洋芋片設計成這個造型呢？雙曲拋物面的標準方程式為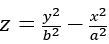，它與三維空間中的xz 平面相交於一條開口朝下的拋物線，與yz 平面相交於一條開口朝上的拋物線，而若是拿一個水平的平面來切這個雙曲拋物面，則會截出一條雙曲線或兩條相交於原點的直線（圖二b 的綠色虛線），因此它才被稱為雙曲拋物面。雙曲拋物面是一種對外在壓力具有較高承受度的曲面，例如我們常見的單側彎曲面（圓柱面的一部分）在左右兩側的擠壓下，很容易會沿著中心線裂開（圖二a）；而雙曲拋物面無論從哪一側擠壓，都比較不容易破碎。

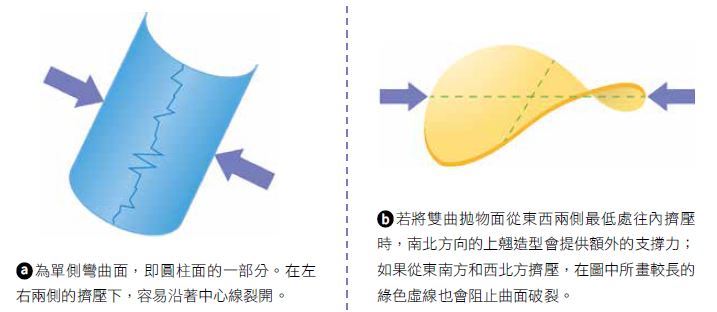
圖二｜雙曲拋物面對壓力的承受能力較高

假設將雙曲拋物面從東西兩側最低處往內擠壓時，南北方向向上翹的造型會提供額外的支撐力；若是從東南方和西北方擠壓時，在圖二b 所畫較長的綠色虛線也會阻止曲面破裂。因此不管從那個方向擠壓，雙曲拋物面都不像單側彎曲面那麼容易碎裂。圖二中的兩條綠色虛線，使得雙曲拋物線更堅固。而事實上，雙曲拋物面上任一點都有兩條直線通過，幾何學家稱這類曲面為「雙直紋曲面」（doubly ruled surface）。直紋曲面（ruled surface，圖三）是指由一條直線在空間中連續變動所掃出的曲面，如果曲面可以由兩條不同的直線各自連續變動而掃出，就會被稱為雙直紋曲面。除了雙曲拋物面之外， 平面（plane） 和單葉雙曲面（one-sheeted hyperboloid）也都是雙直紋曲面。

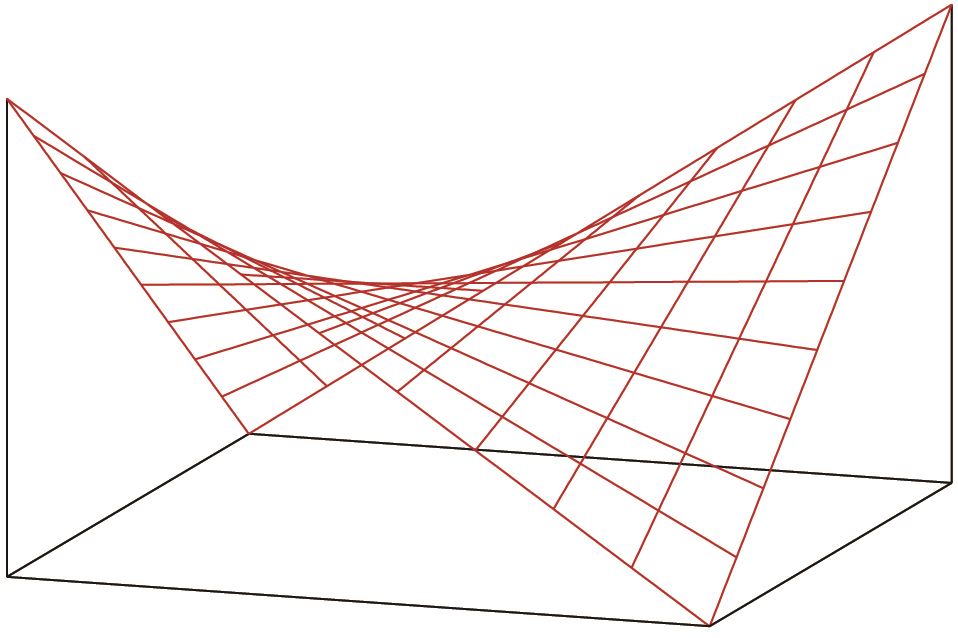
（a）

（b）

圖三：（a）直紋曲面是指由一條直線在空間中連續變動所掃出的曲面，如果曲面可以由兩條不同的直線各自連續變動而掃出，就會被稱為雙直紋曲面；
圖（b）為雙曲拋物面應用於兒童遊樂器材上的實例，圖中的遊樂設施位於高雄市新興國小。
（AndrewHarvey4, Public Domain, Wikimedia Commons；作者拍攝）

只要利用直線型材料就可以建構出直紋曲面，例如 廣州電視觀光塔知名的西班牙建築大師高第（Antoni Gaudí）就運用單葉雙曲面來設計聖家堂（Sagrada Família）的天頂造型（圖四）；而中國第二高塔——廣州電視觀光塔（圖五），本身就是一個巨大的單葉雙曲面。

►西班牙 聖家堂Sagrada Família

圖四：聖家堂大廳屋頂有許多特殊造型，是高第以單葉雙曲面設計而成。（123RF）

►中國 廣州電視觀光塔

圖五：位於中國廣州市的中國第二高塔「廣州電視觀光塔」，其建築本身就是一個巨大的單葉雙曲面。（123RF）

應用於各式建築中的雙曲拋物面設計

每一種直紋曲面的力學特性都不同，例如平面狀的物體容易折成兩半，因此某些品牌的洋芋片會以另一種直紋曲面「波浪面」，增加洋芋片的結構強度（圖六a）。波浪狀或圓弧狀的設計可以協助曲面分散壓力，例如在中世紀前期，火砲引入歐洲之後，許多城牆也都加入圓柱形的設計，不再是一面平直的牆壁，這正是為了利用「圓弧」來分散砲彈的衝擊力（圖六b）。而許多拱門、大教堂的圓頂，以及巨蛋體育館的屋頂也是類似的原理，利用弧狀的結構將屋頂的重量分散到周圍支撐的柱子或牆壁上。

圖六：（a）波浪面的直紋曲面，可以增加洋芋片的結構強度；（b）波浪形的磚牆比一般直線磚牆更不易倒塌。（123RF；Karen Blaha,CC BY-SA 2.0, Flickr）

然而大教堂的圓頂不易施作，且單純的球形屋頂會對下方壁面產生往外的推力，因此需要用其他結構來提供額外的支撐。單就這兩點來說，若要設計屋頂的話，採用雙曲拋物面是比圓頂更好的設計。以設計混凝土曲面建築聞名的西班牙與墨西哥建築師坎德拉（Felix Candela）曾說過：「各種可能的薄殼結構中，最簡單且最實際可造的就是雙曲拋物面。」只要使用條狀的建材就能建構出雙曲拋物面。而除了容易建造之外，以雙曲拋物面作為屋頂造型的最大優點，就是由材料重量所產生的力，可以由向上彎曲部分所產生的張力來拉住，如同吊橋一樣（圖七），這樣就不用在下方設置許多柱子來支撐屋頂的重量，而屋頂的重量也不像圓頂一樣會對整個外牆都產生外推的力（圖八）。目前世界上已經有不少以雙曲拋物面為屋頂的建築，特別是體育館這類需要減少下方樑柱的場所。

圖七｜以雙曲拋物面作為屋頂承受的力
若以雙曲拋物面作為屋頂造型，材料重量所產生的力可以由向上彎曲部分所產生的張力來拉住，就像是吊橋一樣。

►西班牙 奧格拉菲克水族館L'Oceanogràfic

圖八：以雙曲拋物面作為建築屋頂的設計，除了容易建造之外，其最大優點就是由材料重量所產生的力，可以被向上彎曲部分所產生的張力來拉住，因此不用在下方設置許多柱子來支撐屋頂的重量，而屋頂的重量也不像圓頂一樣會對整個外牆都產生外推的力，圖為西班牙瓦倫西亞的奧格拉菲克水族館（L'Oceanogràfic）。
（Felipe Gabaldón, CC BY 2.0, Wikimedia Commons）

找出下一種洋芋片的理想造型？

整體而言，巨蛋型屋頂或雙曲拋物面屋頂，到底孰優孰劣並不容易斷定。因為在這類薄片屋頂建築中，除了考慮力學與建造成本之外，還有材料、風從屋頂上吹過所產生的作用力等因素需要納入考量，還有許多細節必須透過數值模擬才能得知。如果只因為幾何美感或力學考量就設計出各式各樣的屋頂，有時還真的無法在現實中實現。

和洋芋片需要抗壓的需求不同，以雙曲拋物面作為屋頂造型的原因，主要是因為其容易建造且不需額外的支撐，畢竟屋頂只需要防止塌陷，而不用擔心會被人從兩側捏碎。

雙曲拋物面既可以讓洋芋片結構更堅固，又能用來設計成可以實際施作的屋頂，是一個非常特殊的曲面。如果你想製作出新的洋芋片形狀或屋頂造型，那必須先告訴你一件事：數學家已經證明除了平面、雙曲拋物面、單葉雙曲面以外，就沒有其他雙直紋曲面了。因此若是想找到下一個理想的洋芋片造型的話，可能就要多費點工夫囉！

延伸閱讀
1. Félix Candela, The Hyperbolic Paraboloid, The Princeton University Art Museum, 2008. https://artmuseum.princeton.edu/legacy-projects/Candela/paraboloid.html
2. Iasef Md Rian, Fractal-Based Computational Modeling and Shape Transition of a Hyperbolic Paraboloid Shell Structure, Nexus Network Journal, Vol.20:437~458, 2018.