- 精選文章
文章專區
2019-08-01普悠瑪列車為何翻覆？高中物理告訴你
596 期
Author 作者
曾孝明／2016年自清華大學電機系退休後，開始推動高中教育。目前在花蓮縣天主教私立海星中學開授高二數理選進階替代課程。
對軌道車而言，因無駕駛方向盤且又行駛在固定的鐵軌上，火車及捷運等車種，被公認是最安全的大眾運輸工具。其中，普悠瑪號列車是民眾往返北部和東岸最重要又最有效率的交通工具，因此該事故對大眾造成極大的衝擊。
對於此翻車事故，可根據物理定律找出翻覆的原因，並以高中物理知識與牛頓力學進行剖析，讓大眾真正了解事故的真相。而剖析事故的始末，首先要取得足夠且公信的資訊，尤其是完整的行車記錄。《事故報告》內容顯示，在出軌地點的鐵軌上並無有效煞車減速痕跡，列車前方外觀和排障器也無撞擊異物的跡象。報告中提供如車速、列車於各時間的位置、監控系統的數位記錄、出事瞬間駕駛室速度把手的速度刻度段位及煞車把手位置等，這些數據與物證如同飛機的黑盒子，能提供剖析事故發生的原因。
高中物理與牛頓力學分析事故
圖一：列車在彎曲軌道的橫截面概圖。
根據記錄，列車是在彎道發生出軌翻覆事故。藉由等速圓周運動的加速度和曲線半徑R的數學關係式，再根據牛頓運動定律⇀和平面向量，可立即推導，等速v的圓周運動的加速度a的大小為a=v2/R，其運動方向與加速度方向互相垂直。為了產生向心加速度，彎曲的軌道路徑要有內低外高的傾斜面（banked or banking curve）設計（圖一）。理想的情形是，列車僅受到來自垂直方向的重力和來自軌道對列車施加的正向力FN。
mg+FN=ma（1）
a沿著水平方向
如此，鐵軌的橫向並沒受到⇀來自列車的力，而且兩軌道對列車的向上推力相同（FN/2）。在列車運動系統中，快速運動的列車對鐵軌的橫向施力，容易使固定鐵軌的裝置、配件和鐵軌等受損。軌道的傾斜角使外軌高於內軌，在軌道交通專門用語中，此高出的數值稱為超高值（superelevation）。藉由圖一可推導出平衡速率v：
mv2
/R=mg tanθ→v=（gR×tanθ）1/2（2）
當列車停在傾斜的彎曲軌道，傾向倒入內軌，故內軌的受力較大。當列車的行進速率達到平衡速率時，內外軌的受力均等。而超過平衡速率時，外軌的受力較內軌大，若是速率持續增加，內部乘客會感受到來自座椅扶手的推力，兩鐵軌的不平衡受力將更加嚴重，列車運行也更不安全。
列車在彎道時的傾斜角
除了彎曲軌道的傾斜，列車底部的減震彈簧也會在行經彎曲路徑產生傾斜效果（圖二）。太魯閣號與普悠瑪號皆為傾斜式列車（tilting train）；太魯閣號最高速度可達到150 km∕h，依靠「滾珠汽缸式」傾斜裝置，傾斜角可達5度。而普悠瑪號最高速度達160km∕h，利用「空氣彈簧簡易型」車體傾斜裝置，傾斜角達2度。
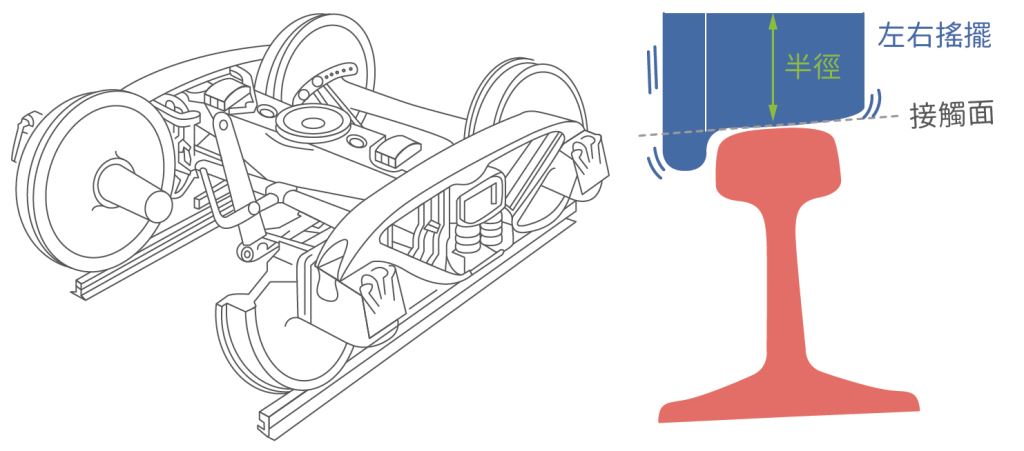
圖二：（左）火車底部簡圖，（右）鐡軌和車輪，其中車輪凸緣比鐡軌表面低。（Department of the Army, Washington DC, Public Domain, Wikipedia）
事實上，普悠瑪號左右搖晃的情況較太魯閣號明顯，但並不影響其行車安全。不同的傾斜裝置取決於製造公司的專利、競爭優勢、市場佔有率、列車售價及鐵路公司的列車保養、維修等因素。在國際間，數家著名的跨國企業都有製造傾斜式列車，例如義大利飛雅特公司（FIAT）的高鐵潘多利諾（Pendolino）列車，其傾斜角雖可達13 度，但由於安全和舒適考量等因素，將傾斜角下修為8度。
另外，《事故報告》提出：「事故列車近武荖坑溪，車速達142 km ∕ h。短短的20秒後，該列車出軌……，武荖坑溪鐵橋段彎道曲線半徑為900公尺，之後為一段長約300公尺直線，接續為曲線半徑300公尺的彎道。」如表一，3種不同車次行經武荖坑溪鐵橋的影像和影像傾斜角度計算結果。
表一：列車通過武荖坑溪鐵橋之影像傾斜角度計算結果。
《事故報告》後續提到：「羅東站至武荖坑溪鐵橋路段的運轉速限，不分車型均為130 km∕h（即曲線半徑R 為900 公尺的速限）；武荖坑溪鐵橋至新馬站路段的運轉速限，太魯閣列車為85 km∕h、普悠瑪為75 km∕h、其他車型為65 km∕h（即曲線半徑R 為300 公尺的台鐵速限）。」陸空交通工具的慣用速率是每小時多少公里，以下是兩速率的換算關係：
1 m/s=（ 1m/1s ）（3600s/1h ）（ 1km/1000m）=3.6 km/h
根據數學式（2）及其他數據，在彎曲軌道中，如果軌道的橫向沒受到列車施力時，不同列車的傾斜角度為表二所述。
一般而言，傾斜式列車比非傾斜列車多出的角度，幾乎是傾斜式列車的傾斜裝置可達到的「額外」傾斜角。但事實
上，傾斜式列車的翻覆臨界時速與上述的傾斜角幾乎無關。上述僅比較曲率半徑300 公尺的傾斜彎道。而如果該事故列車沒有對軌道的橫方向產生作用力，則這列車行經彎道的傾斜角將是
tanθ =(141/3.6 )2 （1/300×9.8 ） =27.56°（3）
如此誇張的彎道面傾斜角對任何鐵路公司是不可能達到的天文數字。換句話說，出事列車不僅對鐵軌的橫方向施加非常龐大的作用力，而且肯定會翻覆！
必定翻覆的傾角與車速
藉由牛頓第三運動定律可充分理解超速列車為什麼會翻覆。等速圓周運動的列車所受的淨力是向心力（centripetal force），因此列車會對外產生大小相同而方向相反的反作用力，此力稱為離心力（centrifugal force）。為了容易理解，在剖析列車於彎道的翻覆臨界速率 vc，暫且先不考慮列車的傾斜角。圖三左為離心力與列車所受到的重力，兩作用力的作用點都落在列車的重心。當離心力達到某一數值（即列車的速率達到某一數值），列車必定翻覆。此刻，列車的旋轉中心點位於外側軌道的車輪凸緣（ ange）和軌道的接觸點。當軌道對列車的作用力落在旋轉中心點，軌道作用力的力臂為0，即毫無軌道作用力的力矩，故圖三沒出示軌道對列車的作用力。
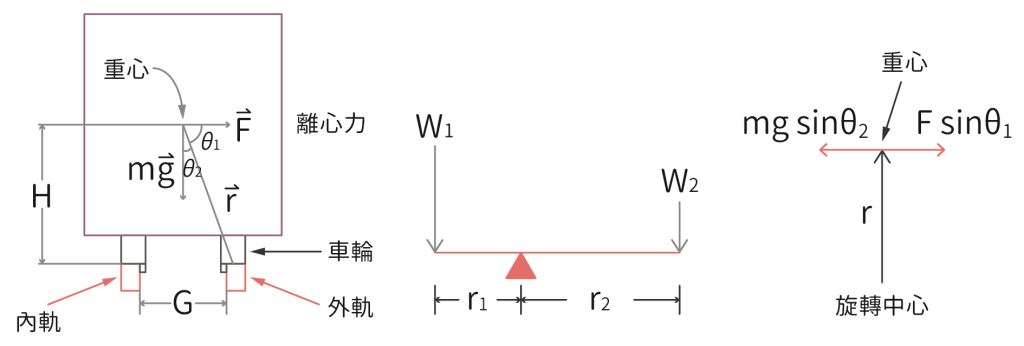圖三：旋轉與力矩（左）、列車參數和橫截面簡圖（中）與蹺蹺板簡圖（右）。蹺蹺板簡圖代表列車速率到達翻覆臨界速率vc，離心力的分力大小等於重力分力的大小。
圖三中的蹺蹺板旋轉是兩力矩作用的結果，平行於旋轉臂（或軸）的力不貢獻旋轉所需的力矩。圖三右則顯示，當垂直於轉動軸（即經過旋轉中心點和列車重心的軸線）的離心力分力大小等於重力在同一方向分力的大小，列車將翻覆，即
(m vc2/R )r×sinθ 1=(mg)r×sin θ2 →( vc2/R )/R sin θ1=g×sinθ 2
θ1+ θ2=90°（4）
當列車速率超過翻覆臨界速率的時候，列車百分之百會向外側軌道方向！
接下來，考慮列車有一傾斜角 ，即把圖三左所提到的車輪凸緣鐵軌道接觸點視為中心，逆時針方向旋轉 （圖四）。相對於水準和垂直方向，有了此小傾斜角，圖三的θ1、 θ2 分別變成 θ1-Δθ 、θ 2+Δθ 。藉由圖三、列車的重心高度H與軌距值G=2L，可以得到：
sin(θ1-Δθ ) = sinθ1 cos(Δθ ) - cos θ1 sin(Δθ ) = (1/r)[H cos( Δθ)-L sin( Δθ)]
sin(θ 2+Δθ ) = sin θ 2 cos( Δθ) + cos θ 2 sin(Δθ ) = (1/r)[Lcos(Δθ )+H sin( Δθ)]（5）
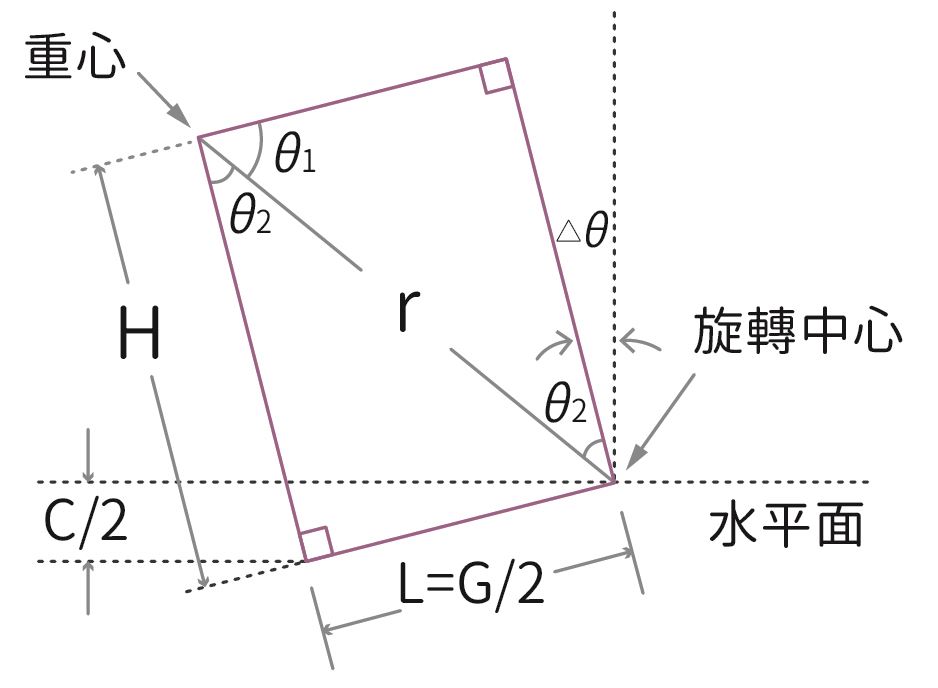圖四：傾斜彎道上列車的横截面簡圖。
無載重列車的重心和軌道面的傾斜角 無關，列車的重心和列車因減震彈簧及其他產生列車傾斜的裝置關係甚微。因此，在式（4）中，用修正後的角度得到列車翻覆臨界速率數學式； vc2R sin（θ1-Δθ ）=g×sin（θ 2+Δθ）；Δθ= 列車的傾斜角度。經簡單的計算，修正的翻覆臨界速率 vc 是：
vc=( gRsin（θ 2+Δθ ）/sin（θ1-Δθ ） )1/2=( gR[L cos(Δθ )+H sin(Δθ )]/[H cos(Δθ )-L sin(Δθ )] )1/2
=( gRL/H [1+H sin( Δθ )/L])/([1-L sin( Δθ )/H])1/2
≅( gRL/H [1+HLsin(Δθ )/L] [1+L sin(Δθ )/H])1/2
=( gRL/H [1+HLsin( Δθ )+ L/Hsin(Δθ )+sin2(Δθ )]1/2
代入普悠瑪號列車的數據，最後兩項可被忽略，可得列車翻覆臨界速率的公式；
vc ≅(gR [L/H+sin( Δθ )])1/2（6）
而從圖四可得知彎道軌道面的傾斜角 與超高值 c 和軌距 G（=2L）的關係；
sin Δθ = c/G（7）
把（7）代入（6），列車翻覆臨界速率vc：
vc=[( G/2H + c/G)gR]1/2( 單位：m/s)
再把秒速換成時速，列車翻覆臨界時速vc：
vc=[( G/2H + c/G) R×9.8×3.62 ]1/2
=[( G/2H + c/G) R×127]1/2( 單位：km/h)（8）
（8）式就是《事故報告》中普悠瑪號列車的曲線翻覆臨界時速。
代入當時事故普悠瑪號列車的數據〔註一〕：
H=1581 毫米、G=1067 毫米、c=90 毫米、R=306 公尺
得到列車傾斜角 、理論翻覆臨界速率vc；sinΔθ = c/G
→Δθ=4.55° & vc=128 km/h
乘客和行李的重量會使列車整體的重心升高，此升高數值應當大於傾斜式列車傾斜裝置產生的重心下降值。簡單來說，此重心改變的修正量並不大。列車在彎道以不平衡時速運行，鐵軌在橫向對列車產生摩擦力，車輪的接觸面略呈現圓錐形。列車的車輪凸緣把列車限制在兩軌道間，凸緣和鐵軌間必須留有一小空間，因此列車運行時有橫向的來回擺動。若是加上此擺動現象，翻覆臨界時速則要再下修。《事故報告》提供日本工程師國枝雅治（Masaharu Kunieda）博士被廣泛被引用的數學公式，把滿載普悠瑪列車的翻覆臨界時速下修14 km∕h，即理論的普悠瑪號翻覆臨界時速約在 114 km∕h。然而，透過各種不同證據顯示，列車當時的時速竟高達141 km∕h ！
在國際間，軌道交通科技和安全是各國都關切的議題。表三為2016 年由日本運輸安全委員會和日本茨城大學研究員共同發表的論文，當中所列出5 種出軌列車的理論估計出軌速率及相關列車資料與數據。其中，瑞士列車在車身未完全通過彎道就已提升速率，其它的列車則是前進至曲率半徑較大之處就出軌翻覆。《事故報告》指出，新馬站鐵軌數據幾乎和福知山線出事地點一致，但是實際上，普悠瑪號的超速值卻比表中任何列車更加的嚴重、離譜！
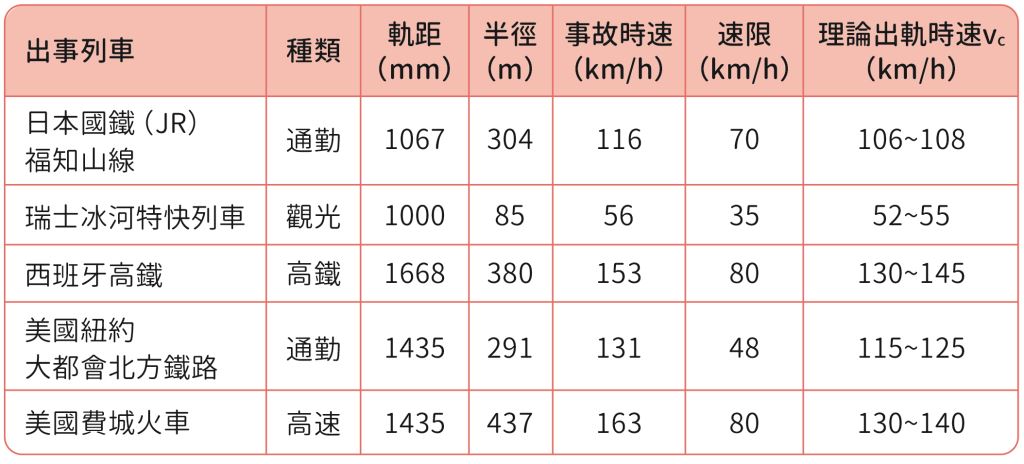表三：5種列車的數據、事故時速和理論上估計的出軌時速 vc。
《事故報告》提到：「事故列車以超過速限的速度進入半徑306 公尺的新馬站彎道，導致列車前進方向第1 節車廂右側車輪浮起後出軌並向左側〔註二〕翻覆，隨後第2~8 節車廂也相繼出軌。」
ATP系統與機車調度員
一般而言，為行車安全普悠瑪號都配備有列車自動防護系統（automatic train protection, ATP）。ATP 可以讀取速限並自動減速，該設計是為防止司機員超速駕駛。但實際上，ATP 的自動減速功能可能會妨礙列車行駛及調度，故某些時候必須隔絕ATP 的忠誠干擾。《事故報告》內容顯示，肇事司機員逕自隔離關ATP，列車時速飆升至141 km∕s，78 秒後列車出軌翻覆。
在遠端機車調度員的主要工作，是提醒司機員不準點的處置方式或前方軌道的異常狀況。不須贅言，在極短的時間內，遠端的機車調度員難以適時又有效阻止司機員超速。舉例而言，飛機飛行期間若出現不正常無法排除的燈號，若找不到機場迫降，則後果可能無法想像，這點和普悠瑪號司機無法排除儀板上異常的燈號完全不同。但是，列車翻覆意外經常是因一些司機員不被嚴重及公開警告的惡習與拚準點文化造成的累積性大禍。這次的普悠瑪號列車完全沒有因機械故障、電子訊號錯誤而直接導致翻覆，唯一原因是超速，肇事司機員的超速逾規定限速值的88％，無庸置疑是在飆火車！
結語
列車在彎道的時速超過翻覆臨界時速必定翻覆是自然界的定律。列車的重心與其是否為傾斜式列車幾乎無關，故翻覆臨界時速利用數學式推導適用所有的列車。臺灣軌道工程學會於今（2019）年3 月22 日，在交通部運輸研究所國際會議廳，舉辦「軌道系統營運安全提升研討會」，被邀請做專題演講的日本大學松本陽（Matsumoto Akira）教授強調：「從事故中得到教育是重要的！」而總頁數多達233 頁的《事故報告》卻幾乎看不到任何的篇幅剖析司機超速必造成列車翻覆，該報告不但直接傷害政府的公信力，也犧牲許多人的權益，這種模糊焦點的官方報告無庸贅言不利未來改革。
必須一再強調，傾斜式列車過彎道時，因列車「額外」的傾斜角度，乘客可在較高的時速下沒有或只感受到少些的橫向力。而傾斜式列車的翻覆臨界時速與列車之該額外角度幾乎無關。當列車時速超過翻覆臨界時速，根據物理定律，列車百分之百會翻覆！
相對於其它國家，臺灣的氣候易使鐵路日曬雨淋，並容易造成鐵道感測器故障。為此，必須找出最佳又經濟的補救方式。筆者認為，或許未來藉由在曲線半徑小的路段加裝類似高速公路的測速和多盞燈的警報裝置，防阻司機員在彎道超速，避免類似的悲劇再次發生。
〔註一〕《調查報告》列出 G=1132 毫米是一項小錯誤。
〔註二〕即外側軌道。
延伸閱讀
1.《臺鐵6432 次列車新馬站內正線出軌事故調查事實、原因及問題改善建議報告》，https://reurl.cc/7zk5d。
2. A. Matsumoto, Y. Michitsuji and Y. Tobita, The Dynamics of Vehicles on Roads and Tracks, Cagliari, Italy, 2016.