- 專欄
文章專區
2024-05-01歐拉示性數 每一面都是六邊形的球體有可能存在嗎?
653 期
Author 作者
俞韋亘/中央大學數學系副教授,研究專長為離散幾何。
Take Home Message
•歐拉示性數可驗證球面上的多面體是否存在於三維空間,計算公式為V-E+F=2,V為點的個數,E為邊的個數,F則是面的個數。
•歐拉示性數證明在三維空間中,正多面體的數量僅有五種,分別是正四、六、八、十二、二十面體。
•每個面都是六邊形的球體,有n個面、2n個點、3n條邊,代入公式後會得到2n-3n+n=0,於是根據歐拉示性數,它不可能存在。
近日在動漫《葬送的芙莉蓮》(葬送のフリーレン)中出現的防禦魔法,是個每一面都是「六邊形」的球體。此圖案一出現後,隨即有數學愛好者表示這是現實中不可能存在的形狀。然而一般大眾或許不太能理解,為什麼這樣的形狀不可能出現?會不會只是他們信口雌黃,也許努力嘗試一下,其實可以畫出這種形狀的球體?如果真的不存在的話,有什麼數學定理或工具可以證明嗎?
在數學上還真的有定理可以說清楚它不存在的原因。本文將以歐拉示性數(Euler characteristic),證明這樣每個面都是六邊形的六角形球體不可能存在。
(劉與佳繪製)
歐拉示性數
在正式開始講解證明前,筆者先介紹一下什麼是歐拉示性數。
一個球面上的多面體必須滿足以下公式:
V-E+F=2
其中,V(vertex)是點的個數,E(edge)是邊的個數,F(face)則是面的個數。若以文字表示的話就是「點個數減去邊個數加上面個數必須等於二」。該公式最早由法國數學家笛卡兒(René Descartes)於1635年證明,但當時較不為人知。之後瑞士數學家歐拉(Leonhard Euler),也於1750年獨立證明了這個公式。1860年,人們發現笛卡兒在過去也曾證明此公式,因此將該公式命名為歐拉-笛卡兒公式。
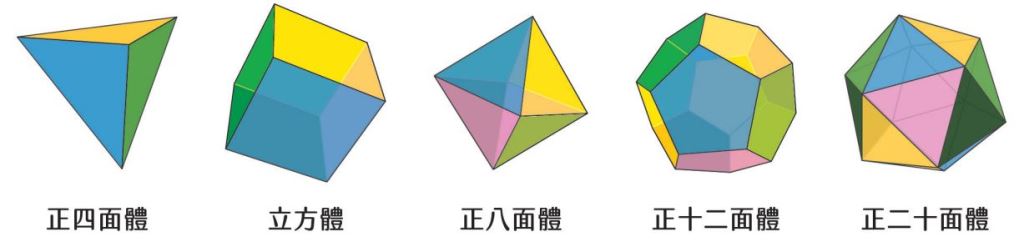
我們舉幾個例子驗證歐拉-笛卡兒公式。例如底下五個空間中的正多面體,正四、六、八、十二、二十面體都會滿足歐拉-笛卡兒公式。
(Image by pikisuperstar on Freepik)
正四面體也就是正三角錐,每一面皆為正三角形,它有4個點、6條邊、4個面,所以代入公式後:4-6+4=2,正確無誤。再來看看正六面體。正六面體其實就是立方體,具有8個點、12條邊、6個面,所以代入公式為8-12+6,結果也會是2。若還是不太相信的讀者,也可以再試著算算看正八面體、正十二面體、正二十面體帶入歐拉-笛卡兒公式後算出來的結果,可以發現這五個正多面體都滿足歐拉示性數(表一)。事實上,球面上的任意多面體都必須滿足歐拉示性數,並不侷限於正多面體。
表一|正八面體、正十二面體、正二十面體的點、線、面個數(資料來源:作者提供)
|
點
|
線
|
面
|
V-E+F
|
截面形狀
|
正八面體
|
6
|
12
|
8
|
2
|
三角形
|
正十二面體
|
20
|
30
|
12
|
2
|
五角形
|
正二十面體
|
12
|
30
|
20
|
2
|
三角形
|
由於歐拉已經證明球面上多面體的點線面個數必須滿足此這公式,如果不滿足就代表它必定不存在。因此我們可以再回頭看看六邊形球體,只要套用公式檢查它的V-E+F是否等於2,就可以知道它是不是真的存在。首先假設這個六邊形球體有n個面,而且每一面都是六邊形,再來思考一下它會有幾個點?理論上會有6n個點,因為每一個面都是由6個點形成的六邊形。再仔細觀察一下此六邊形球體,每個點有幾條邊?答案是3條,也就是說每一個點是被3個不同的六邊形共用。所以我們必須除以3,所以實際上會有2n個點。
緊接著,我們要考慮邊的數量。理論上因為有n個面,且每個面都是六邊形、有六條邊,則一共有6n條邊。但我們一樣必須考慮重複計算的部分。觀察一下,每條邊被幾個六邊形共用?答案會是2。也就是每條邊都被重複算了兩次,因此我們將6n除以2,也就得到3n條邊。
最後來整理一下數據,我們假設了六邊形球有n個面,然後根據「點」被共用三次,「邊」被共用兩次,計算後就會得到V=2n(2n個點),E=3n(3n條邊),F=n(總共n個面)。代入公式後得到2n-3n+n=0,答案顯然並不等於2。於是根據歐拉示性數,每個面都是六邊形的多面體不可能存在於球面上!
三維空間中有多少正多面體?
另外,歐拉示性數也可以用來證明,在三維空間中只存在五種正多面體,分別就是前面討論過的正四、六、八、十二、二十面體,這五個正多面體也有人稱呼為「柏拉圖立體」(Platonic solid)。正多面體必須長得很規則,每個面都要是一模一樣的正多邊形,且每個邊長都一樣長,每個點連出去的邊個數一樣多。所以我們不妨先假設每個面都是正k邊形、每個點都有d條邊。假設我們現在有F個面,每個面都是正k邊形,所以一共有F×k條邊,但是每條邊都被兩個面共用,所以要除以二。於是邊的個數就是E=Fk/2,則F=2E/k。接著考慮每個點都有d條邊相連,總共有V個點,又因為每條邊都被兩個點共用,所以總共有E=Vd/2的等式,所以V=2E/d。
最後再把這兩個等式代入歐拉示性數:
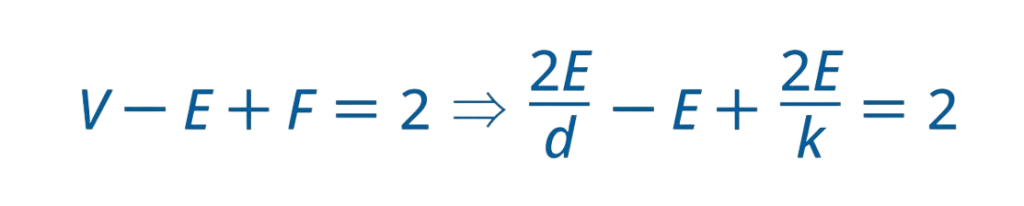
兩邊共除2E再移項一下可以得到
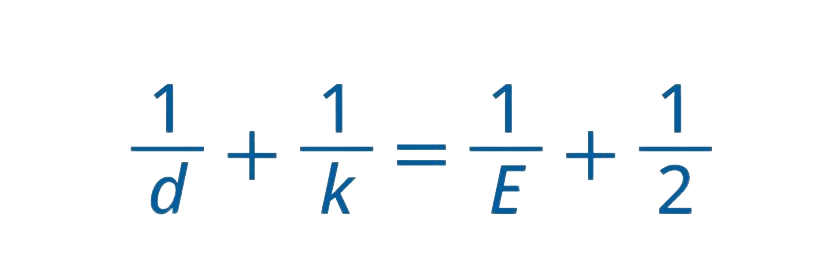
由於E是整個正多面體邊的個數,所以一定是正整數,因此1/d+1/k>1/2,d與k必須是正整數且大於2。但也不能太大,因為倒數和必須大於1/2,所以d、k不可能都同時大於4。那麼d、k至少有一個是3或4,嘗試一下便可以找出所有滿足1/d+1/k=1/E+1/2的正整數解,就是(d,k)=(3,3),(3,4),(4,3),(3,5),(5,3)。這五種解就分別對應到正四、六、八、十二、二十面體。
舉例來說,正四面體就是(3,3),每個點有三條邊相連,每個面是正三角形;正六面體是(3,4),每個點有三條邊,每個面是正方形(k=4);正八面體是(4,3),每個點有四條邊,每個面是正三角形。剩下兩個,我們留給讀者自行確認。究竟(3,5)、(5,3)哪個是正十二面體,哪個又是正二十面體呢?其實這兩個結構具對偶關係,也就是可以把點和面的情形互換,而正六面體、正八面體也有類似的關聯性。
生活處處皆數學
我們希望藉這個例子讓讀者體會與想像歐拉當年有多厲害,可以證明球面上多面體的點線面個數必須要滿足此等式。在距今大約300年前,也就是1750年時,歐拉就證明了這個公式,對應到中國歷史上的年代是清朝乾隆15年。如果再考慮笛卡爾證明此公式的1635年,那就是明朝末年,比1644年清兵入關還早。當時東西方的數學程度差距,可見一斑。
至於歐拉怎麼證明出這個公式,在數學的分類裡此證明過程屬於拓墣學(topology)的範疇。由於難度、篇幅的限制,本文沒有提到太多拓墣學知識,有興趣的讀者可以自行搜尋看看歐拉示性數。過往在教授三維空間只有五種正多面體時,筆者都會使用歐拉示性數來驗證三維空間中正多面體的數量。而這次出現在動漫中的六角形球體,同樣能用此公式證明它不存在。希望讀者能藉此有趣,並且體會到生活中無處不數學,連看動漫時都可以引發出歐拉示性數的證明。最後,也希望讀者可以仔細挖掘與觀察生活周遭的事物與問題,會發現生活處處都是數學!

歐拉在距今大約300年前,就證明了歐拉示性數公式,可見當時西方的數學發展已達到一定程度。(Jakob Emanuel Handmann, public domain, Wikimedia Commons)