- 專欄
文章專區
2024-04-01找出數據中的統計規律 中央極限定理的奧祕
652 期
Author 作者
張明中/中央研究院統計科學研究所副研究員,研究興趣為如何從大量的數據空間挖掘細微的資訊。
Take Home Message
•記錄、分析擲骰子獲得的點數,我們可以了解均勻分布、獨立事件、常態分布,以及中央極限定理等統計觀念。
•中央極限定理是統計的核心和基礎,它說明了在極度隨機的條件下,只要集合夠多的獨立隨機變量,統計結果將趨於常態分布。
•中央極限定理能用於計算民調樣本支持率的統計誤差,估算群體支持率的信賴區間,作為我們在繁雜複雜的數據中預測、決策的依據。
日常生活充斥著不確定性,而這些不確定性也深刻地影響著我們。舉例來說,即使氣象預報顯示降雨機率僅有20%,我們出門時還是有可能會意外地遇到下雨;有時候前一天身體狀況還好好的,但到了第二天卻突然咳嗽不止;在學業上,同樣的會考成績在去年或許足以讓你進入心儀的第一志願,但今年可能就只夠進入次選學校。這些不確定性的現象背後由多種複雜的因素交織而成。即使是投擲一個公正的骰子,每一次投擲出現的點數也都無法預先確定。因此,統計科學(statistical science)正是運用機率理論來描繪和預測這些不確定性現象的學科。基於對歷史事件的觀察,統計科學提供對未來最可能且不確定性最小的預測,進而成為從過去經驗中學習的重要工具。
統計科學之所以有如此能力,很大程度上得益於眾多賦予了它強大解釋和預測能力的基礎理論。在這些理論中,有一個最核心和基礎的定理⸺中央極限定理(central limit theorem)。簡單來說,中央極限定理說明了就算在極度隨機的條件下,只要集合足夠多的獨立隨機變量,它們的結果將會趨於常態分布(normal distribution)。此發現不僅是統計科學的基石之一,也是我們在面對繁複世界時理解和處理不確定性的關鍵。透過中央極限定理,我們能從看似混沌的數據中提煉出有意義的模式和趨勢,從而在不確定性之中找到確定性的線索。
統計學中的常態分布
常態分布又稱高斯分布,是統計科學中最常見的機率分布類型之一。如果對機率分布不太熟悉,可以先將它粗略地想像為一大堆數字所繪製出的直方圖(histogram),也就是將很多數字依大小排列,而後計算每個數字出現的頻率,最後將這些頻率畫出圖表。這個圖表會展示不同數字出現的頻率分布,形成所謂的直方圖。你可以在圖表中看到哪些數字出現得多,哪些比較少,從而獲得對數據集整體特性的直觀理解。
常態分布圖形呈現對稱的鐘形曲線,其中大部分的數據集中在期望值(expectation, μ)附近,並隨著距離期望值的增加而快速減少(圖一)。另一個常態分布的關鍵參數是標準差(standard deviation, σ),它描述了數據分布的寬度,也就是數據離散程度的度量。此外,還有一種特殊的常態分布稱為「標準常態分布」(standard normal distribution),它的期望值為0、標準差為1。
這種標準化形式使得不同的常態分布可以透過簡單的變換相互比較,這在統計分析中極為重要。藉由將任意常態分布的數據轉換為標準常態分布,不同的數據集可以在相同標準下進行有效比較。在一個標準常態分布中,約有68%的數據落在期望值的一個標準差範圍內,95%落在兩個標準差範圍內,99.7%落在三個標準差範圍內。
而在我們的日常生活中,常態分布就像是無形的規則,無處不在。例如多數人的身高都集中在一個普通範圍,特別高或矮的人不太常見;學校的考試成績中,大部分學生的分數都圍繞在班級的平均分,那些特別高分或低分的同學就比較少;甚至是在超市消費時,大部分人的支出都差異不大,真正花費大手大腳或特別節儉的則相對少見。這些生活化的小事,都展示著常態分布在我們生活中的普遍性和重要性。
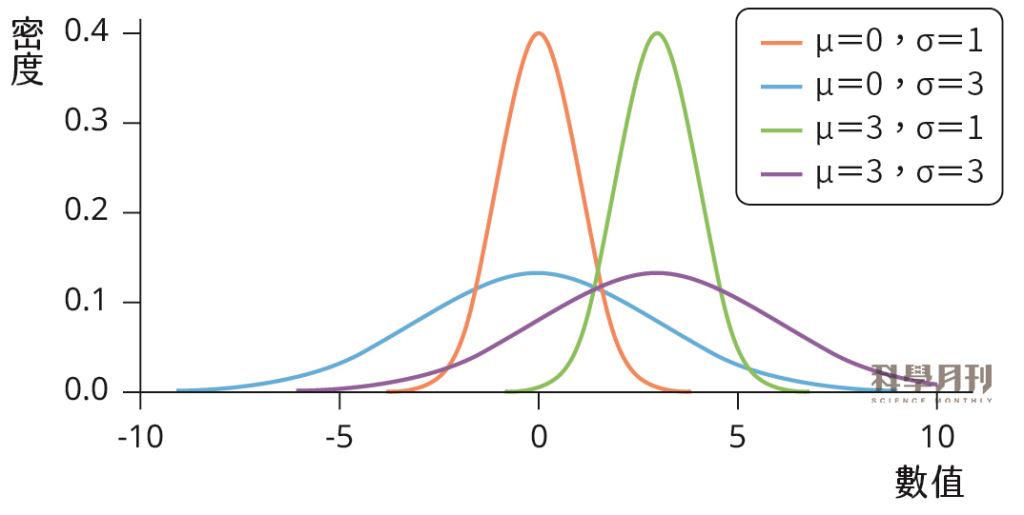
圖一|常態分布與不同期望值、標準差的統計函數分布圖
以四種不同參數設置的常態分布機率密度函數。這些分布的μ和σ分別以不同顏色表示,其中橘色代表標準常態分布。μ決定了分布的中心位置,而σ則決定了分布的寬度。(資料來源:作者提供)
擲骰子遊戲
想要深入理解中央極限定理,需要較深的機率理論基礎。在本文中,我們可以透過簡單的「擲骰子」實驗來示範中央極限定理的原理。一般常見的骰子是正方體,六個面分別印有數字1~6。在骰子公正的前提下,投擲一次,每個面朝上的機率均為1/6。假設連續投擲骰子一萬次,並記錄下每次的點數,將會得到一萬個介於1~6的數字。如果將這一萬個數字製作長條圖,你會發現數字1~6出現的次數相差不大(圖二a)。這個結果在骰子公正的情況下,並不令人意外。……【更多內容請閱讀科學月刊第652期】