- 專欄
文章專區
2024-03-01超過300年的「倍立方」探究之旅 古希臘人對平方軌跡的探索
651 期
Author 作者
單維彰/中央大學數學系、師資培育中心、文學院學士班合聘教授。
Take Home Message
•古希臘人認為必須用真解——也就是幾何方法,而不是測量才能求出真解,並且為了解決倍立方問題研究平方軌跡。
•平方軌跡的一般形式是y2=ax,其中a是一個給定的正量,也就是某個指定的線段,稱為「標準桿」。
•在阿波羅紐斯、帕布斯等人的努力下,找出了許多平方曲線的性質,此曲線也在光學、重力學領域有重要應用。
不曉得讀者是否曾聽過這種說法:「古希臘的數學不重實用而重理論,這個特徵流傳到歐洲造就了西方文明。」筆者在這裡想要提議另一個看法,結果一樣但原因與過程略為不同。筆者認為古希臘數學並無不重實用的意思,他們研究數學的初心也具有實用目的⸺酬神,也就是答謝神或取悅神。在一個相信神能斷定死生禍福、管控風雨雷震的社會裡,還有什麼比酬神更實用、更要緊的文化活動?
古希臘的數學確實獨步於其他文明,但起因是他們認為必須用「真解」酬神。例如想要將一塊正方形的地基放大一倍,也就是從一平方單位變成二平方單位,希臘的匠師或地政幕僚應該能夠像其他文明的同儕(例如巴比倫、印度、中國),知道要把原正方形的邊長放大成1.41倍。可希臘的神職人員、菁英分子知道那是有瑕疵的量,並不是真解。他們知道要以原正方形的對角線為邊長去做出新的正方形,那才是真解。他們當然明白,一旦在地上畫出對角線,做直角畫出正方形地基肯定會產生誤差。但沒關係,那是人間的瑕疵,在「屬神」的純粹世界裡,他們的幾何方法是沒有瑕疵的真解,而這才是神給他們的考驗。
找出「倍立方」問題的解答
基於同樣的宗教信念,當希臘人面臨「倍立方」問題:將一座正立方體神殿的體積放大一倍,也就是從一立方單位變成二立方單位,他們也不能接受坊間工匠的方法⸺把原立方體的邊長放大約1.26倍,而必須使用幾何方法。這就讓古希臘菁英展開了為期約300年的長途探究。
最早的突破性概念是將x3=2「擴編」為x4=2x,然後令x2=y,則y2=2x。如果可以沿著互相垂直的兩條線畫出x2=y和y2=2x這兩條「平方軌跡」,則兩條軌跡的交點就能決定真解x的線段(圖一)。
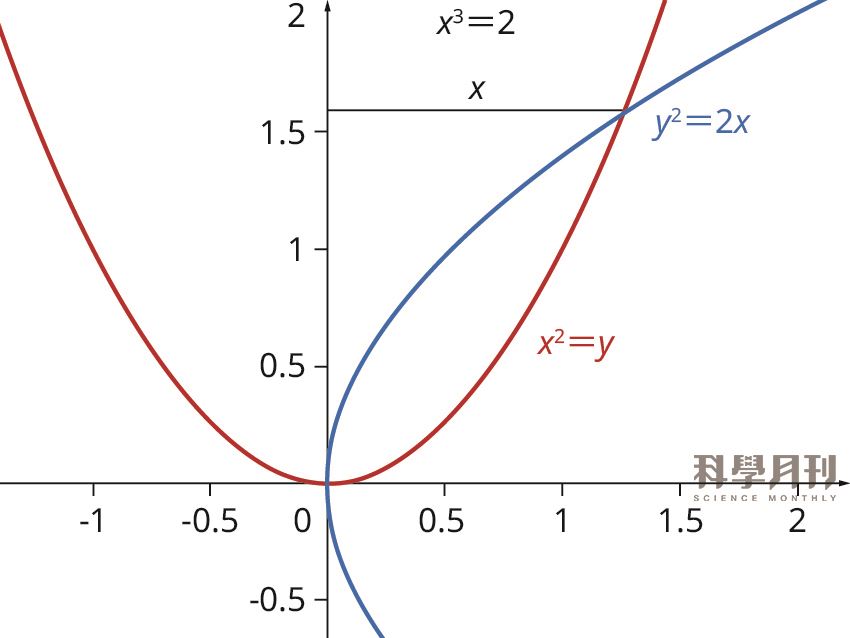
圖一|沿著互相垂直的兩條線畫出x2=y和y2=2x這兩條「平方軌跡」,則兩條軌跡的交點就能決定真解x的線段。(資料來源:陳玉芬)
由於古希臘人沒有代數符號、方程式、直角坐標系,他們全用文字和比例關係來思考和溝通,過程相當繁複。但筆者相信現代人(至少我自己)應該沒有耐心閱讀古希臘的忠實翻譯,因此下文皆直接以現代符號表示。順帶一提,當數學講二次函數的時候寫y=x2,但是講拋物線的時候卻是寫x2=y,這兩條等式不是一樣嗎?它們確實一樣,但是把拋物線寫成x2=y已經是2000年以來的習慣。
古希臘的菁英社群(包括神職人士)追求真解,所以要杜絕測量且堅持以尺規作圖,並特別強調「尺」沒有刻度,只能用它畫線而不能用它測量。但他們一時找不到作x2=y的尺規畫法,所以不稱它為圖形(graph),而稱為軌跡(locus)。軌跡是由滿足某些條件的點聚集而成的曲線或曲面,若用現代話語來說,軌跡就是方程式在坐標平面或坐標空間中對應的圖形。……【更多內容請閱讀科學月刊第651期】