文章專區

Take Home Message
•在長頸鹿斑紋和海龜殼中的圖像紋理，藏著俄羅斯數學家沃羅諾伊所提出的一種空間分割演算法則，又稱沃羅諾伊圖。
•在平面上點出一些離散點，將這些點以順時針方向依序畫出三角形並找出三角形外心，最後連接外心就能畫出沃羅諾伊多邊形。
•沃羅諾伊圖可應用於摺紙、瓷磚、彩繪玻璃等圖像，創造出兼具空間配置與強健結構的作品。

 
你是否想過，自然界中某些生物身上習以為常的紋理或是地景排列結構，如長頸鹿斑紋、海龜殼、蜻蜓翅膀、蜂巢結構、泡泡排列方式等，究竟是隨機產生或是依循某種規律法則？

蘊含數學法則的沃羅諾伊圖

想要理解這些圖案紋理當中的法則，就一定要提到沃羅諾伊圖（Voronoi diagram）。這是一種由俄羅斯數學家沃羅諾伊（Georgy Voronoy）提出的空間分割演算法，透過此演算法分割出來的空間配置，竟意外地與某些大自然的圖案紋理有著極為相似的表現。只要依循這個規則，就代表著我們可以透過沃羅諾伊圖找出自然界的這些圖案紋理，並重現與長頸鹿身上的塊狀圖案完全相同的圖形。
 
那麼，沃羅諾伊圖要如何繪製？程序如下（資料來源：作者提供）：
➊在平面上點出一些離散點（分割點）。

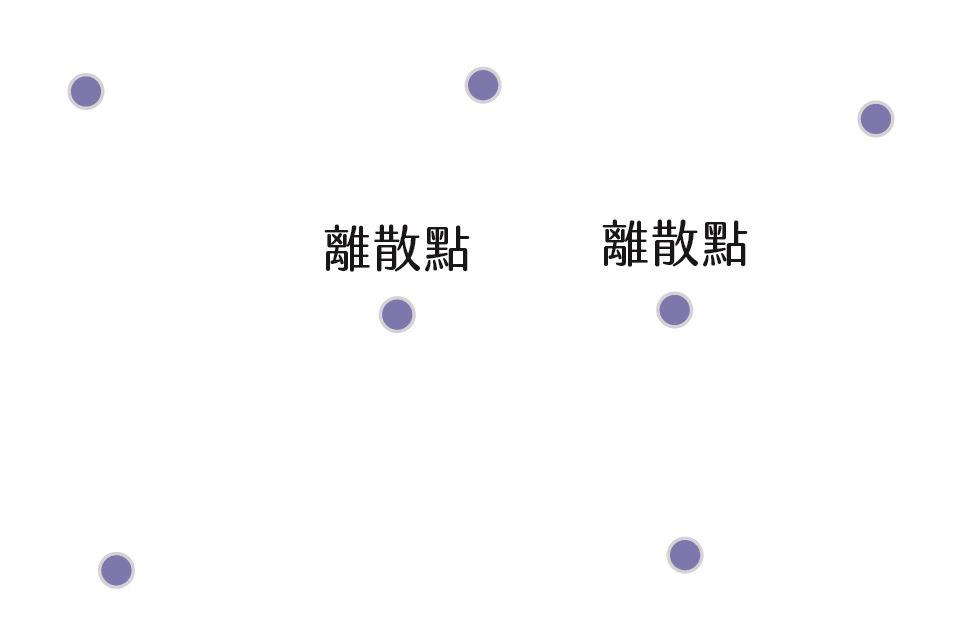
➋將這些離散點按照順時針的方向依序畫出三角形。

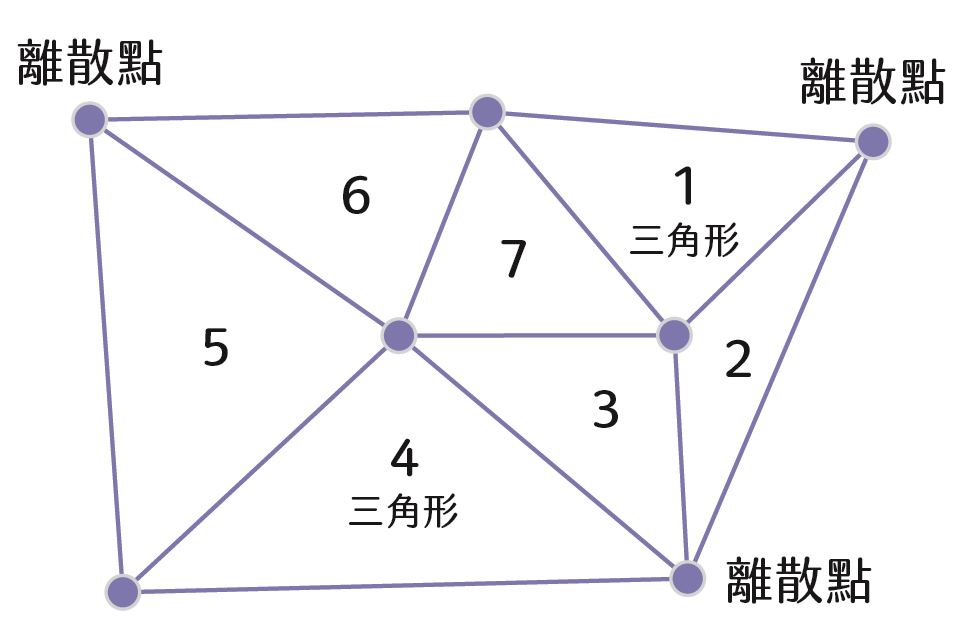
➌將這些三角形，利用畫出每一邊的中垂線來找出三角形的外心〔註〕。

 

〔註〕銳角三角形的外心會在三角形的內部，直角三角形的外心會在三角形的斜邊上，鈍角三角形的外心會在三角形的外部。

➍最後將外心連接在一起就是「沃羅諾伊多邊形」（Voronoi polygon），又稱 「泰森多邊形」（Thiessen polygons），也就是由沃羅諾伊演算法分割出來的空間。

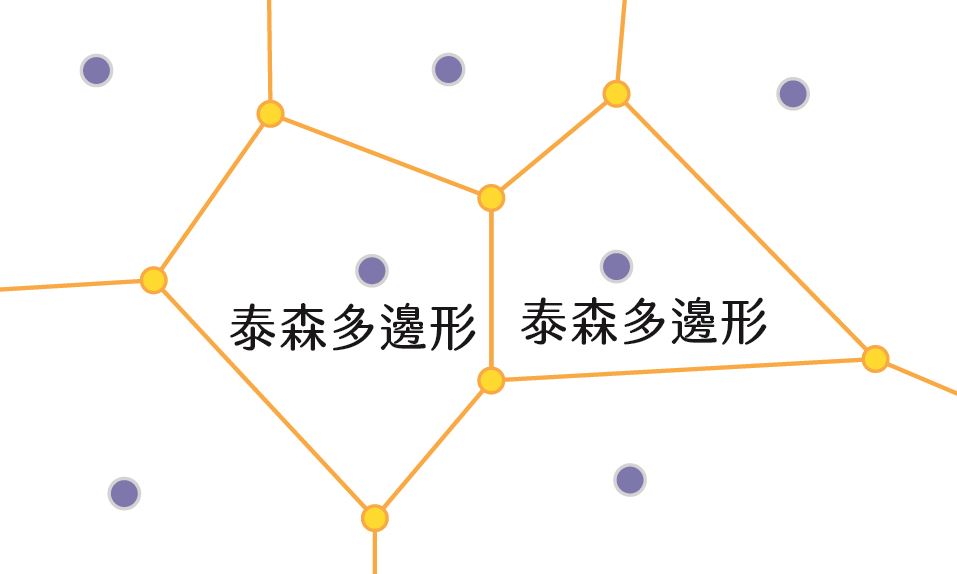
泰森多邊形有什麼特別之處？首先最大的特點為泰森多邊形全都是凸多邊形；第二項特點為泰森多邊形內的任一點，與自身離散點的距離會比與相鄰多邊形的離散點近；最後一項特點為泰森多邊形邊上的點到兩側的離散點距離相等，此特性也呼應了上一點的說明，邊上的點分屬兩個相鄰多邊形，因此與自身離散點最近的距離剛好會與相鄰的離散點距離相同。

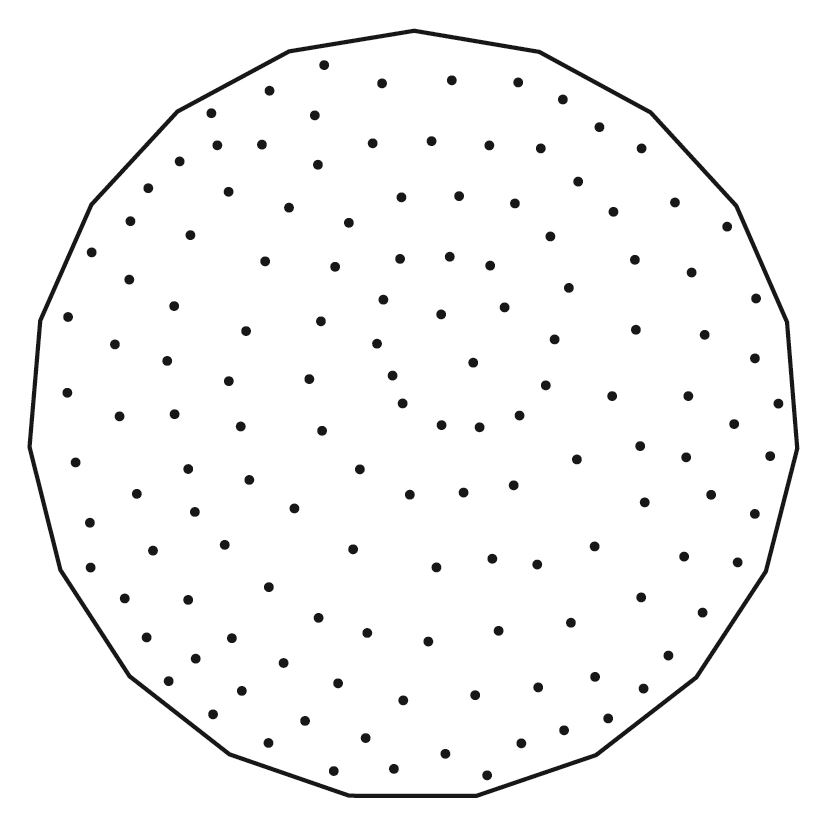
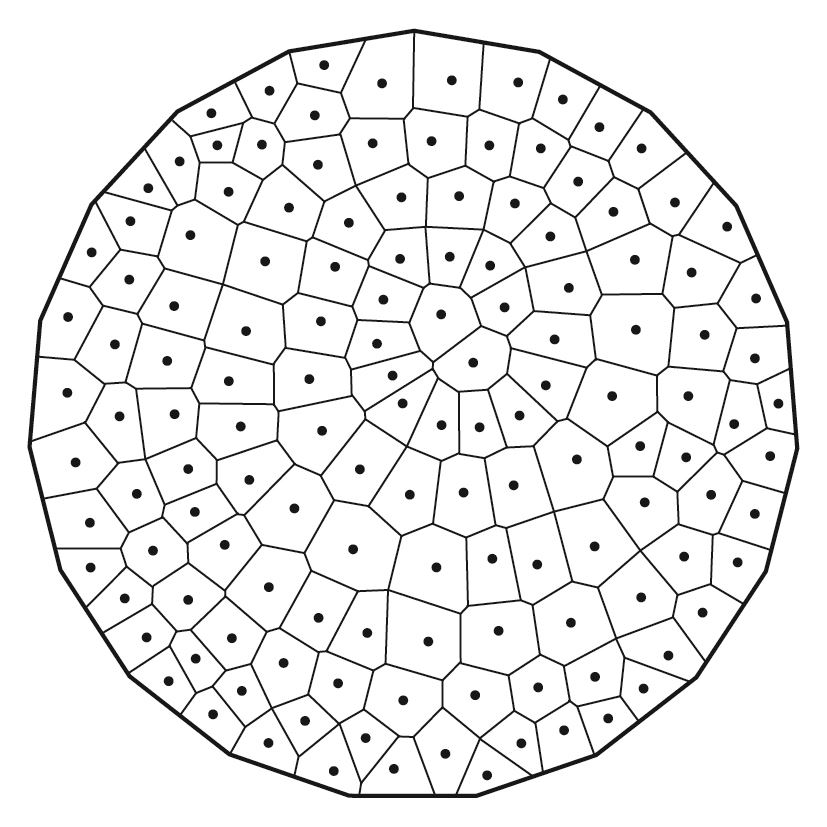
透過簡單的程式就可以畫出整個沃羅諾伊圖，如筆者的作品〈沃羅諾伊的猜想2〉，就是當離散點變多的時候產生的沃羅諾伊圖。這是一種將沃羅諾伊圖應用於藝術創作上的成果，透過這個作品我們也可以提出另一個摺紙猜想⸺是否所有沃羅諾伊圖中的多邊形都可以用摺紙的方式摺出相對應的多邊形紙盒呢？（簡稱為沃羅諾伊的摺紙猜想）。以下圖為例，圖中一共有137個離散點：
 
➊在正19邊形中，隨意點出137個離散點（分割點）。

➋透過沃羅諾伊演算法畫出的沃羅諾伊圖，圖中共有137個泰森多邊形。

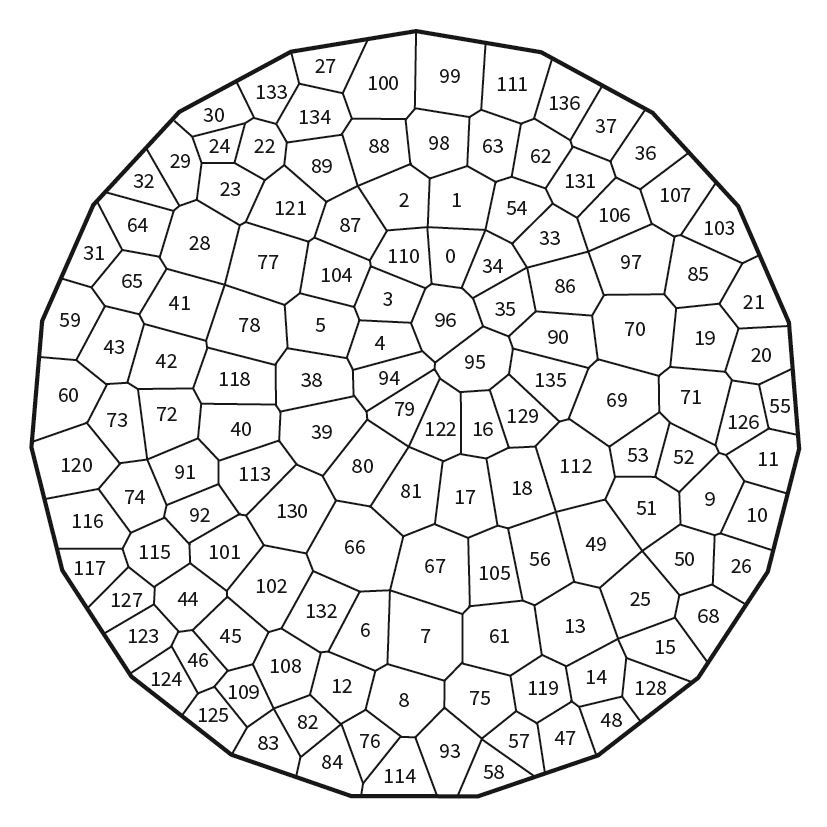
➌將點出的離散點標上編號，以利完成137個多邊形紙盒時，可以作為拼接回來的參考圖。

 
而若是要摺出多邊形紙盒，實際作法可分成兩種：只用長方形的紙摺製（沃羅諾伊猜想1）或透過裁切成多邊形外形的紙摺製（沃羅諾伊猜想2）。

以七邊形作為拼接形狀的〈沃羅諾伊的猜想1〉（作者提供）


以紙材創作的〈沃羅諾伊的猜想2〉（作者提供）


以光雕投影創作的〈沃羅諾伊的猜想2〉（作者提供）

用長方形的紙摺製

第一種方式的限制比較多，必須要是具有內心的多邊形，也就是需要用具有內切圓的多邊形才可以。但要如何得知多邊形是否具有內心呢？內心是指多邊形的每一條角平分線會相交於內切圓的圓心，但並非每個多邊形都會有內切圓。內切圓代表內心與每個邊的垂直距離相等，也就是如果可以從多邊形的每個邊上皆找出一個點，且從這些點畫出的垂直線剛好互相交在同一點，則這個點的位置就是內心。
 
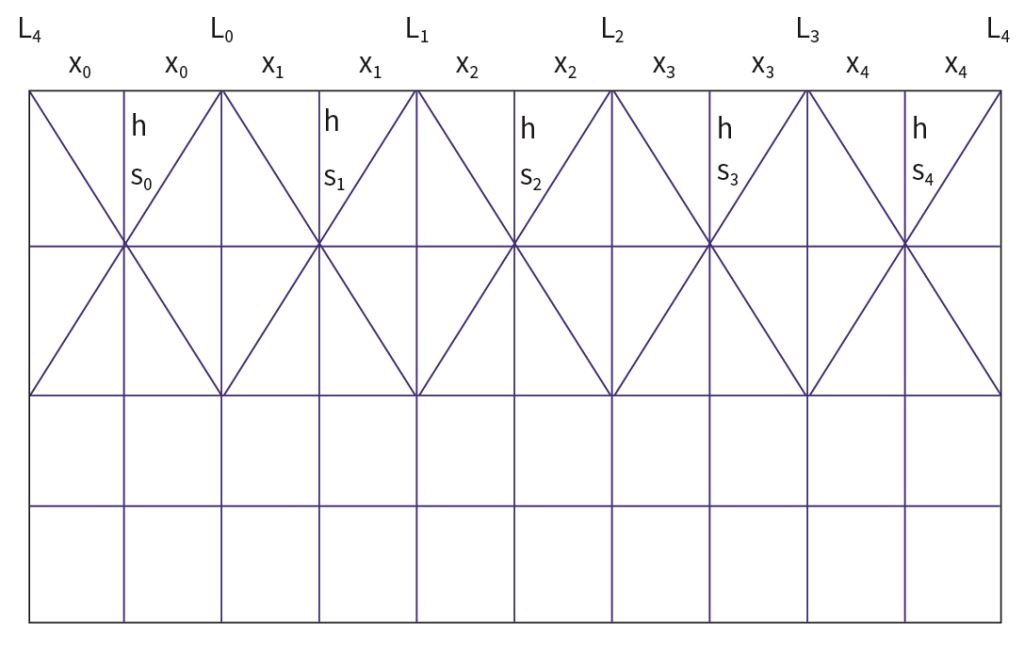
找出邊與內心垂直距離的方法，會使用到角平分線的平分角（s）與該邊端點的距離（x），而垂直距離（h）就是tan(s)＝x/h，所以x＝h×tan(s)。舉例來說，如果有一個五邊形，那麼就會有x₀/tan(s₀)＝x₁/tan(s₁)＝…＝x₄/tan(s₄)，x₀＝h×tan(s₀), x₁＝h×tan(s₁),…, x₄＝h×tan(s₄)，同時因應角平分線的條件，假設每個邊長分別為L₀, L₁, … , L₄，就會有L₀＝x₀＋x₁, L₁＝x₁＋x₂, L₂＝x₂＋x₃, … , L₄＝x₄＋x₀，其中s₀, s₁, … , s₄、L₀, L₁, … , L₄是已知的條件，因此可以推得L₀＋L₁＋L₂＋L₃＋L₄＝2ⅹ(x₀＋x₁＋x₂＋x₃＋x₄)，也就是L₀＋L₁＋L₂＋L₃＋L₄＝2ⅹ(h×tan(s₀)＋h×tan(s₁)＋…＋h×tan(s₄))，為了找到一個可以滿足以上方程式的垂直距離h值，我們可以在整理後得到：h＝(L₀＋L₁＋L₂＋L₃＋L₄)/(2ⅹ(tan(s₀)＋tan(s₁)＋…＋tan(s₄)))。
 
計算出的h值，需要再滿足以下的條件：
L₀＝x₀＋x₁＝h×tan(s₀)＋h×tan(s₁)
L₁＝x₁＋x₂＝h×tan(s₁)＋h×tan(s₂)
L₂＝x₂＋x₃＝h×tan(s₂)＋h×tan(s₃)
L₃＝x₃＋x₄＝h×tan(s₃)＋h×tan(s₄)
L₄＝x₄＋x₀＝h×tan(s₄)＋h×tan(s₀)
 
若可以找到符合條件的h值，則代表這個多邊形具有內心，同時也可以算出多邊形內心的座標，藉此畫出第一種摺法的摺線圖。
 
若s₀, s₁, … , s₄、L₀, L₁, … , L₄ 是已知的條件，則摺線圖及結果如下圖。

透過裁切多邊形外形的紙摺製

第二種摺法可以摺出各種多邊形，再透過畫出等比放大的多邊形，並將它裁切就可以摺出多邊形的紙盒。
 
除了摺紙之外，沃羅諾伊圖也可以應用於密鋪瓷磚中。如果將上方的照片圖像轉換成沃羅諾伊圖多邊形上的顏色，也能製作如彩繪玻璃、馬賽克般的沃羅諾伊圖，或透過摺紙的方式完成實體的沃羅諾伊圖作品。

以裁切成多邊形外形的紙摺出紙盒

▼將沃羅諾伊圖中的1、2多邊形等比放大並繪製出摺線圖（資料來源：作者提供）

以上兩種多邊形紙盒的摺法，可以應用在需要製作不規則多邊形紙盒或容器時。

從大自然到幾何設計的奧妙

從探索自然界中的出現過的圖像紋理到運用的演算法重現出沃羅諾伊圖，在過程中體驗到自然界運行依循的其實是一種平衡原則。因此，如果我們可以將沃羅諾伊圖應用在各種設計的需求上，將會展現另一種創意的設計法則。像是建築結構、裝置造型的設計，最終設計出可以配置空間同時又兼具強健的結構。
 
另一方面，如果將沃羅諾伊圖視為一種密鋪設計，也就是像多邊形瓷磚設計一般，那麼將會為牆面帶來多樣化、獨一無二的客製化設計。另外，不只是瓷磚形狀，彩繪玻璃、拼圖的圖塊形狀等設計，也都是可以發揮創意的方向！

（Photo by Randall Ruiz on Unsplash）
 

進入連結：https://cartography-playground.gitlab.io/playgrounds/triangulation-delaunay-voronoi-diagram/，透過電腦程式實際繪製、觀察製作中圖像的變化，更能夠理解沃羅諾伊演算法的重點並畫出泰森多邊形！