文章專區

Take Home Message
• 等差數列是一種在數列中每兩個相鄰項之間的差相等，也就是具有「公差」的數列。除了課本的公式之外，等差數列還有許多你不知道的故事。
• 質數與等差數列看似毫不相關，不過澳洲數學家陶哲軒與英國數學家格林提出的「格林－陶定理」，卻證明質數裡面包含任意長度的等差數列。
• 任意長度等差數列的討論始於1926 年，荷蘭數學家范德瓦爾登等人曾討論過「博德猜想」，在討論的過程顯示這個猜想應該是對的，最後也成功證明。

大家在求學時期一定學過「等差數列」。舉例來說，臺北市東區有一棟28層的大樓電梯發生故障，因此大樓的管理階層想召集一個應變會議，每層樓都需要派一位代表參與討論。已知每層樓都有可以使用的會議室，假設每一位與會代表每向下走一層樓的不滿意度為1，每向上走一層樓的不滿意度為2，舉行會議的這一層樓與會代表的不滿意度為0。為了讓所有與會的樓層代表的不滿意度總和達到最小，請問會議應該在第幾層樓舉行？

我們先假設會議在第n層樓舉行，則第n＋1 層樓的與會代表要往下走1 層，他的不滿意度為1；第n＋2 層樓的與會代表要往下走2 層，他的不滿意度為2；依此類推，從第n＋1 層樓到第28 層樓的與會代表不滿意度將構成數列1, 2, 3,…, 28－n，這是一個以1 為首項、1 為公差、共有28－n 項的等差數列。另一方面，第n－1 層樓的與會代表要往上走1 層，他的不滿意度為2；第n－2 層樓的與會代表要往上走2 層，他的不滿意度為4；依此類推，從第n－1 層樓往下到第1 層樓的與會代表的不滿意度也會構成數列2, 4, 6,…, 2(n－1)，這是一個以2 為首項、2 為公差、共有n－1 項的等差數列。只要再分別將上述兩個等差數列的各項相加，就是等差級數1＋2＋3＋…＋(28－n) 和2＋ 4＋ 6＋…＋2(n－1)。兩個級數各別求和後，將兩個結果加起來，得到一個有n 的式子，再想辦法找一個n 使得答案達到最小，就可以求出解。等差數列除了在數學課本學到的公式外，還有一些你可能未曾聽過的小故事，接著就讓我們來看看各種與等差數列有關的趣聞或定理吧！

等差級數求和－自幼聰慧的高斯

據說在德國數學家高斯（Carl Friedrich Gauss）小時候，他的數學老師為了讓教室裡的小朋友安靜下來，便出了一道算術題目，要求學生們計算1 ＋ 2 ＋ 3 ＋…＋100，而且還說算對的人就可以提前先回家。不過出乎這位老師意料之外的是，才一會兒功夫，高斯便將他的小黑板放在講桌上，那上面沒有任何算式，只寫著一個數字「5050」，這是高斯給的答案。老師非常驚訝，就請高斯解釋答案從何而來，他回答道：「我發現這個級數非常有規律， 那就是1＋100＝101，2＋99＝101，3＋98＝101 等，依此類推直到50＋51＝101。因為總共有50 組加起來等於101的數對，所以總和就是50×101＝ 5050。」今天的國中學生都知道下列等差級數和的公式：對於每一正整數n，恆有

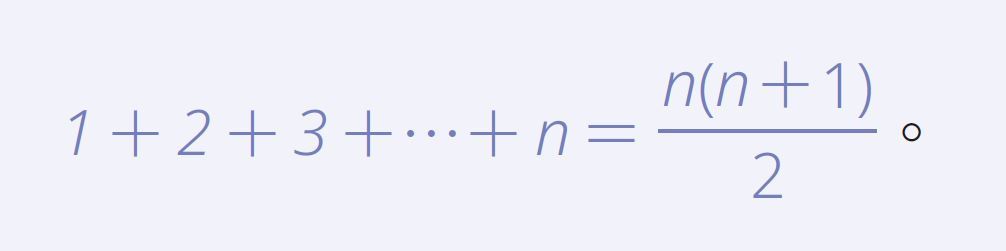
這個公式有很多種證明方法，下圖是筆者最喜歡的一個「無言」證明。

圖中的第1列1個、第2 列2 個、…、第n 列n 個，總共有 Sn 個實心圓，構成直角三角形。若將這個形狀旋轉180° 則成為有Sn 個空心圓的直角三角形，兩者合在一起成為邊長分別是n 和n ＋ 1 的矩形，共有n(n ＋ 1) 個圓。可以得到2Sn ＝ n(n＋ 1)，而有 Sn ＝ n(n ＋ 1)/2。

菲爾茲獎的光環－天才數學家陶哲軒

除了等差數列以外，質數也是一個基礎的數學概念。有趣的是，這兩個看起來似乎不相關的概念，其實也可以湊在一起講出一些數學。一個自然數如果可以寫成其他兩個自然數的乘積a＝bc，則稱a 是b 和c 的倍數，稱b 和c 是a 的因數。一個比1 大的自然數，如果除了1 和自身之外沒有其他因數，則稱它為質數。例如2, 3, 5, 7,11, 13, 17, 19, 23 都是質數，但是4 並不是質數，因為它有1, 2, 4 這三個因數。質數的性質自古以來便被許多人研究，例如希臘時代數學家歐幾里得（Euclid）證明了「質數有無限多個」；質數的漸進分布定理「不超過x 的質數個數π(x) ≈ xln x」則是由高斯最先發現，後來在1896 年由法國數學家阿達瑪（Jacques Hadamard）和比利時數學家瓦萊布桑（Charles Jean de la Vallée Poussin）先後獨立給證明。

來到20 世紀，故事的主角陶哲軒（Terence Tao）是第二代澳洲香港移民，……【更多內容請閱讀科學月刊第643期】