- 科技報導
文章專區
2020-12-15古典電腦不能做到的事，讓量子電腦來吧！
468 期
Author 作者
宇津木健、德永裕己（監修）
古典電腦不擅長的問題為何？
使用一般的電腦，通常應該不會解不了困難的問題或計算遲遲不結束。然而，大規模模擬、密碼、最佳化等領域，有許多對古典電腦來說「解不了的問題」。本文解說對古典電腦而言，什麼樣的問題「解不了＝不擅長」。
可在多項式時間內解決的問題
首先，這裡所謂古典電腦不擅長的問題，一般定義為「尚未找到多項式時間解法」的問題。（圖一）。
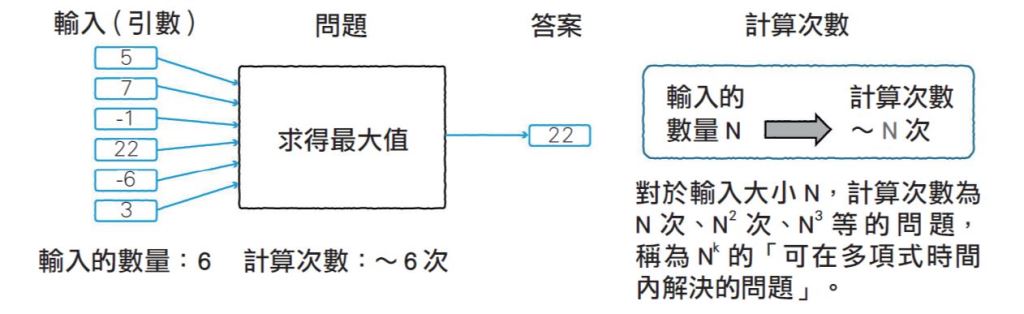圖一：能求解的問題示意。
無論什麼樣的問題，一定有輸入。以程式來說便是引數。而所謂能解決的問題，是指對於輸入（引數）的數量（輸入的大小）所需計算的次數不致太多的問題。舉例來說，「從輸入的數字當中求得最大值」這個問題，當輸入的數字為6個時，如果使用逐一比較大小關係的計算來進行，大概需要計算6次來求得解答。輸入的數字為10個則為10次、100個則為100次，因此問題「求得最大值」的計算次數，是對於輸入大小N來說需要N次的計算。
此外，「求得輸入數字的總和」也是N次；「從輸入的數字當中選出餘數最大的一對數字」則是像循環賽一樣計算所有兩兩成對，大約需要N2次等。我們周遭的問題大多可以Nk（k：整數）的多項式來推估計算次數。像這樣大約Nk次的計算次數之問題，由於能以N的多項式來推估計算時間，因此稱為可在多項式時間內解決的問題。
尚未找到多項式時間解法的問題
另一方面，尚未找到多項式時間解法的問題是什麼樣的問題呢？舉例來說，假設問題為「對於輸入的數字，求得最接近乘積為40的組合」。應該如何求解呢？一般的思考方式是，寫出輸入的數字的所有組合，計算它們的乘積，找出最接近40的組合吧。若輸入的數字有6個，將有26=64個組合。也就是說，需要進行64次乘法計算來找出最接近40的組合。像這樣求解，當輸入的數字有10個時為210=1024 次、20個時為220=1048576次、30個時為230=1073741824次，不斷增加（圖二）。
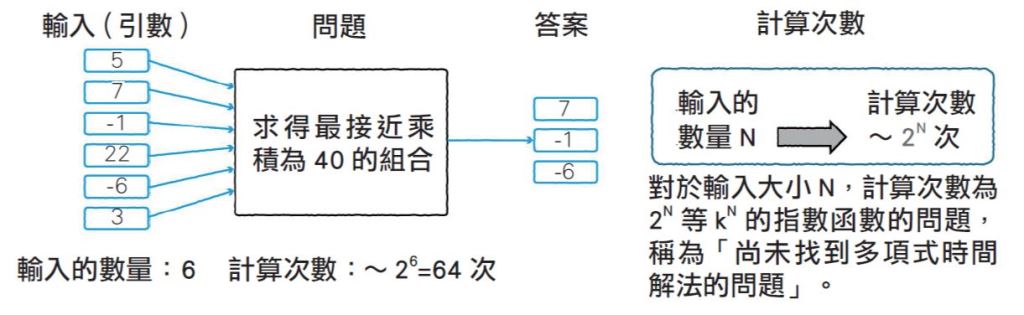圖二：解不了的問題示意。
對於輸入大小N，可能需要kN（k：整數）次的計算次數，也就是當N逐漸變大，計算次數可能以指數函數逐漸增加（需花費指數時間）的問題，便是尚未找到多項式時間解法的問題，稱為古典電腦不擅長的問題。對於這樣的問題，可期待量子電腦能發揮長處。圖三顯示對於輸入大小N的計算量（計算次數）。計算次數通常以Order（符號：O）表示。可以發現對於N的多項式時間與指數時間，隨著N變大，明顯看出計算次數將有很大的差距。
圖三：對於能求解的問題與解不了的問題之問題輸入大小（引數數量）N之計算次數（0為表示計算次數Order的符號）。量子電腦擅長的問題為何？
那麼，量子電腦可發揮長處的問題究竟是什麼樣的問題呢？本節說明期待量子電腦達成的效果。
量子電腦可發揮長處的問題
首先，經常列舉的古典電腦不擅長的問題，包括「組合最佳化問題」、「質因數分解、密碼破解」、「量子化學計算」、「機器學習裡的學習」、「複雜物理現象的模擬」等。其中有「幾項」是量子電腦可發揮長處的問題。這裡需要留意的是，並非古典電腦不擅長的問題全部能用量子電腦輕易解決，而是在古典電腦不擅長的眾多問題裡，一部分可能藉由量子電腦高速求解（圖四）。因此，量子電腦也不容易解決的困難問題當然比比皆是。世界各地的研究者正在研究可用於量子電腦的量子演算法。下面介紹各種方式的範例。
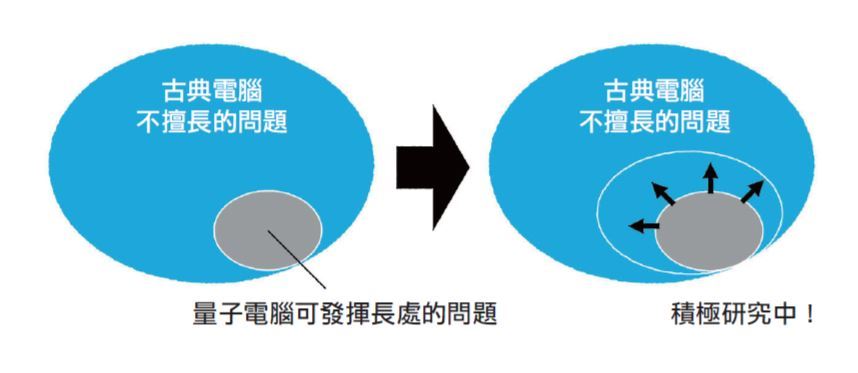圖四：量子電腦可發揮長處的問題。
期待不久的將來可達成的效果
這裡介紹運用量子電路模型和量子退火預期可分別在不久的將來達成的效果。
．量子電路模型
關於量子電路模型的量子電腦，世界各地的企業和研究機構正持續進行研究開發。特別是現在朝著實現數十至數百個量子位元，加速研發。這種數十至數百個量子位元的量子電腦，預期可用於量子化學計算和機器學習。
量子化學計算用於藥品的開發和新材料的開發。開發新藥和高功能材料時不僅要反覆實驗，如果能藉由計算來預測實驗結果，可以在短時間內有效率地進行開發。然而，為了以良好的精度進行量子化學計算，必須盡可能不要用近似的方式計算量子力學方程式，對古典電腦來說將是非常大的計算量。量子電腦得以有效率地執行這種龐大的計算，現在正在進行相關的量子演算法研究。
此外，也期待量子電腦在機器學習領域大顯身手（圖五）。現在看來掀起熱潮的機器學習，正是處理龐大計算量的問題。使用稱為量子機器學習的量子電腦來強化機器學習的量子演算法研究，正蓬勃發展。
圖五：可期待量子電腦（量子電路模型）的領域。
．量子退火
至於量子退火，D-Wave Systems已經實現了2000量子位元的量子退火機，從量子位元數來看，量子退火機似乎比量子電路模型的進展更快。然而，D-Wave Systems的量子退火所使用的量子位元，與現階段量子電路模型所用的相比，在稱為相干時間（coherence time）的保持「量子性」的時間上，亦即量子位元的壽命，是比較短的。相對地，其特徵是實作大規模的量子位元數比較容易。
使用2000量子位元的量子退火機，可以解決小規模的組合最佳化問題。所謂組合最佳化問題，是從眾多的組合當中找出最好的組合，應用廣泛。比如說，藉由搜尋物流的最短路徑，預期能降低成本或紓解壅塞等。這類問題在社會層面很重要，卻很難用古典電腦有效率、高精度求解，因此期待能用量子退火盡可能求得精度更好的解答。此外，正在進行的還包括將量子退火應用於機器學習的研究（圖六）。
組合最佳化 機器學習（抽樣）
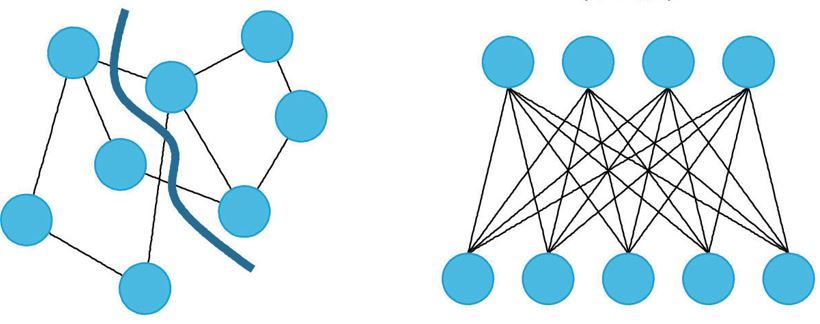圖六：可期待量子退火的領域。
利用量子退火機的特性來進行機器學習，特別是應用於稱為「抽樣」（sampling）部分的研究也正在進行。
目前的2000量子位元能處理的問題僅限於小規模。但今後若能有更多的量子位元，並延長相干時間，開發出提升量子位元之間的結合和控制精度的量子退火機，應用範圍也會更廣（圖七）。不過，隨著量子位元數增加，需要考量抗雜訊能力降低等問題。
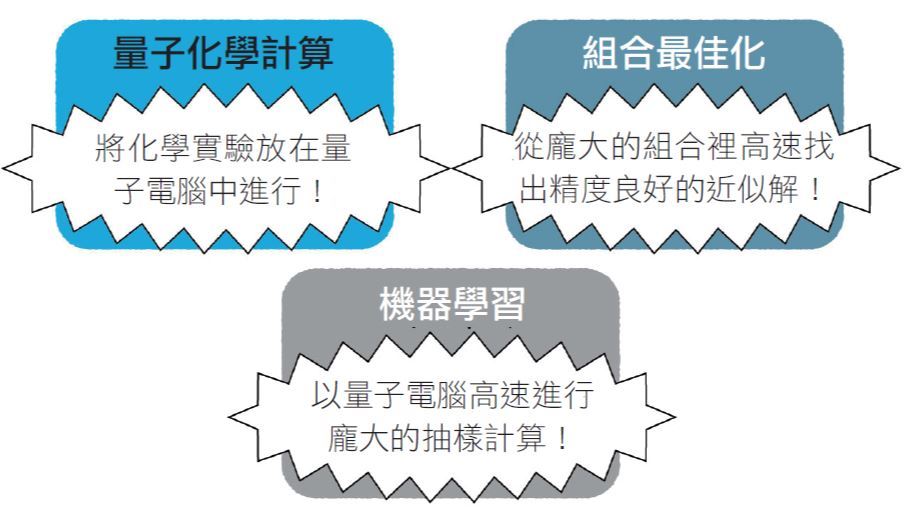
圖七：期待量子電腦的領域。受到矚目的背景
最後，介紹近來量子電腦備受矚目的三項原因（動機）（圖八）。
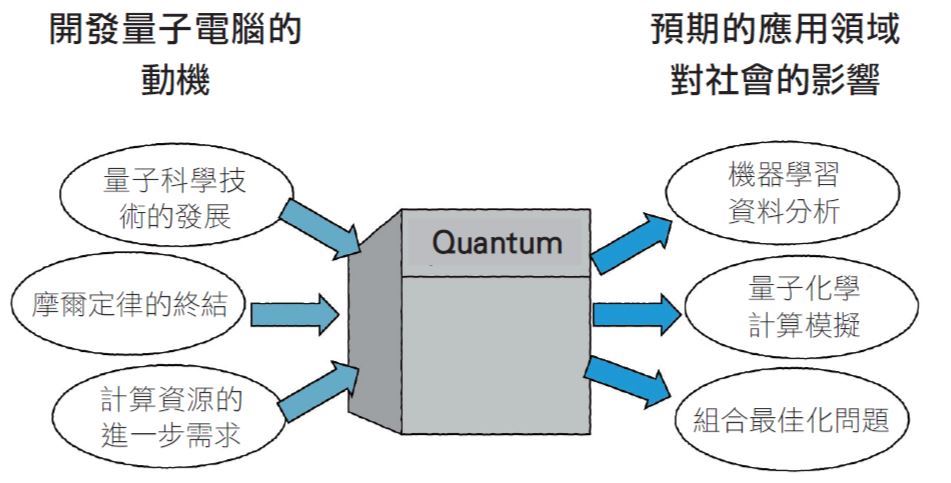
圖八：量子電腦受矚目的原因。
第一項原因是「量子科學技術的發展」。2012年，諾貝爾物理學獎頒發給法國的阿羅什（Serge Haroche）和美國的瓦恩蘭（David J.Wineland）。兩人獲獎的理由是「研究能夠量度和操控個體量子系統的突破性實驗方法之成就」。這項研究的意義在於，得以用實驗室方式控制量子力學的狀態。換言之，這兩位科學家是以實驗室的方式控制量子位元的先鋒。2000年前後，兩人取得成為其獲獎原因的研究成果，其後歷經近二十年至今，相關研究迅速發展，全世界都在進行量子位元的研究開發，進展到至少能進行計算、嘗試可在雲端運用的程度。這項量子技術的成熟，正是量子電腦受到矚目的背景。【更多精彩內容，請看《圖解量子電腦入門：8堂基礎課程+必懂關鍵詞解說，從計算原理到實務應用、通訊到演算，破解讓人類大躍進的科技新浪潮》一書（臉譜出版）。】
書 名∣《圖解量子電腦入門：8 堂基礎課程+ 必懂關鍵詞解說，從計算原
理到實務應用、通訊到演算，破解讓人類大躍進的科技新浪潮》
作 者∣宇津木健、德永裕己（監修）
譯 者∣莊永裕
出版社∣臉譜
出版日∣ 2020 年11 月7 日
• 深入說明量子電腦的原理、量子演算法的運作，第一次學習就上手；
• 精闢剖析量子電腦的發展沿革、現況與願景，一次弄懂量子電腦的全貌；
• 涵蓋量子物理、資訊理論、計算機科學尖端研究，貫通量子電腦基礎知識；
• 圖像化解說關鍵詞彙和重要概念，讓困難的理論變得簡單易懂；
• 日本尖端研究專家專業分析當下和未來的量子電腦應用。
2016年，歐盟發表「量子宣言」；2018年，美國總統簽署《國家量子計劃法案》；2019年，臺灣大學IBM量子電腦中心成立⋯⋯。科技強權、資訊龍頭全球競逐，量子知識霸權爭奪戰已然開打，各行各業都需要瞭解量子電腦。
本書旨在成為貫通量子電腦的嚮導，含括量子電腦的各類知識。為了讓非專家的讀者無礙地理解，以簡明的方式解說相關詞彙和重要概念。從最入門至較深入的內容，透過圖像化的說明，讓困難的理論變得容易瞭解。