- 封面故事
- 2020年
- 612期－2020諾貝爾獎特別報導（12月號）
文章專區
2020-12-01時空的奇異旅程
612 期
Author 作者
卜宏毅／清華大學物理所博士。目前為臺灣師範大學物理系助理教授及天文重力中心成員，研究興趣為黑洞天文物理。
今年諾貝爾物理獎的一半獎項，由英國數學物理學家潘洛斯獲得，他自1960年代開始為廣義相對論、宇宙論及黑洞等研究屢屢提供卓越的貢獻。此外，還有許多概念也由他的名字命名，例如用來研究時空結構的潘洛斯圖（Penrose diagram），以及抽取黑洞旋轉動能過程的潘洛斯過程（Penrose process）等。而本次潘洛斯獲獎的主要原因為「黑洞是廣義相對論的直接結果」，其中包括了在重力塌縮到某個程度時，必然會形成時空奇異點（singularity），也因此造成了黑洞。時空奇異點是時空曲率無限大的一個時空結構，卻也是在廣義相對論架構下是無法進一步解釋的可能時空特徵。潘洛斯是怎麼得到這樣的結論呢？讓我們看看這精彩的歷史發展。
史瓦西解是偶然嗎？
時間回到1915年，愛因斯坦提出廣義相對論描述重力為彎曲時空的效應，以及彎曲時空與「場源」關係所對應的「場方程式（Einstein field equations）」。在該理論提出的數個月後，德國數學家史瓦西便找出第一個場方程式的解：史瓦西解。史瓦西解是一個球對稱的時空解，時空中所有的質量都聚集在半徑為0的地方。儘管時空其他地方都是真空狀態，在其圓周長能符合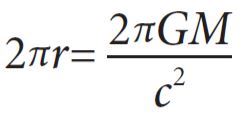
（G為萬有引力場數；M為天體質量；c為光速）的球面形成了一個「有去無回」的時空邊界，稱為事件視界（event horizon），一旦進入這個的邊界，就再也無法回到邊界外部了。
最初人們對於史瓦西的想法爭論不休，直到1939年，理論物理學家歐本海默（J. Robert Oppenheimer）與他的學生史奈德（Hartland Snyder）計算一個球對稱天體的重力塌縮結果，果真得到了如史瓦西解描述的時空結構。然而，這是否意味著大自然真的允許形成一個密度無限大的奇異點？包括愛因斯坦在內的反對方開始懷疑，此結果是否只因為計算中考慮了球對稱的完美假設呢？
利用囚陷曲面解釋黑洞奇異點的形成
直到1960 年代，宇宙給了人們黑洞存在的暗示：天文觀測發現了存在於宇宙早期的天體，卻也因此需要一個能有效產生能量的機制。廣義相對論的重要開拓者惠勒（John Wheeler）等人開始重新思考黑洞存在的可能性：如果黑洞真的存在，那麼黑洞附近的物質會緩慢且穩定地掉入黑洞，而此過程中所釋放的龐大能量將是極為自然的解釋。於是惠勒和潘洛斯討論這個問題，使潘洛斯捨棄了球對稱的假設，改用時空拓墣概念來探討重力塌縮時所產生的奇異點，並在1965年發表論文。之後他也與霍金（Stephen Hawking）合作討論了在宇宙生成時也必然存在一個奇異點。
潘洛斯利用囚陷曲面（trapped surface）探討時空的演化，以解決奇異點的形成問題。他發現一旦重力塌縮過程中產生囚陷曲面，奇異點就會不可避免地產生。
囚陷曲面是一個二維的曲面，例如一個包圍著坍縮中天體的球面，我們以圖一中的一維黑色圓圈來類比囚限曲面的概念。如圖一上方，假如黑色圓圈上的每一點都朝著半徑向外的方向射出一道光（藍色箭頭），這些光線所形成的藍色圓圈，會比原本的黑色圓圈較大；類似的概念，若黑色圓圈上的每一點都朝著半徑往內的方向射出一道光（紅色箭頭），紅色圓圈則會比黑色圓圈較小。在A點與B點，向內與向外的光所包圍著的黃色區域稱為光錐，其限制了速度不超過光速的物體能在時空中的運動範圍。
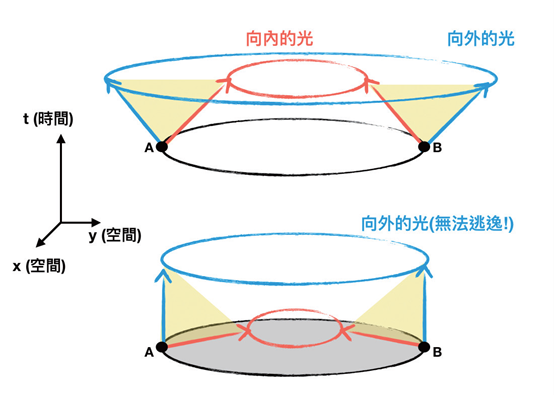圖一：囚陷曲面示意圖
本圖是利用光線探討時空結構。藍色與紅色圓圈分別是由黑色圓圈上的每點都沿著徑向往外及往內射出的光線所組成，如A 點與B點出發的藍色與紅色箭頭所示。上方的時空圖中，黑色圓圈內沒有包圍住足夠的物質，藍色圓圈比黑色圓圈大，紅色圓圈則比黑色圓圈小。但有沒有可能藍色圓圈不會大於黑色圓圈呢？當光線行進因為受到黑色圓圈包圍住的物質（用圓圈中塗滿的灰色表示）所影響時是有可能的，下方的時空圖就是一個範例。當光錐（黃色部分）因為重力導致的時空彎曲而足夠傾斜時，即使是向外發射的光也無法逃逸，這就是囚陷曲面產生的條件。潘洛斯發現，一旦重力塌縮過程中產生囚陷曲面，就會產生奇異點與黑洞。（作者繪製）
而圖一下方則顯示了光線的行進方向受到圓圈內足夠大的重力「吸引」，使朝向外發射的光所造成的藍色圓圈不一定比黑色圓圈要大，導致A、B兩點所構成的光錐範圍傾斜，即使是向外發射的光線也無法逃逸。……【更多內容請閱讀科學月刊第612期】