- 專欄
文章專區
2014-08-01Lissajous曲線
536 期
Author 作者
游森棚 ∕ 任教臺灣師範大學數學系。
全國科展的季節又到了。擔任評審多年,每年數學組都有研究軌跡的作品——在圖形中讓某些量變動,然後觀察某個特殊點的軌跡。這類的問題,除非軌跡要出奇不意有趣,或者要有好的性質,否則容易成為孤立的觀察,最後變為冗長求方程式的計算,失了問題的本意。
這個月的專欄來介紹一個中學師生不太熟悉,但非常美麗的軌跡。我記得老科學教育館有一個裝置:一個漏斗懸掛在一組桿子之下,把沙子裝在沙漏中,桿子和沙漏擺動,漏下的沙子就會在地面上畫出一個曲線。比如,讓沙漏繞圈圈旋轉,漏出來的沙子軌跡就是一個圓。
想像一下我們拿著一條線,底部掛著沙漏。顯然,如果沙漏像單擺左右擺動,則沙子的軌跡就是來回重複的線段。但科教館的裝置要實驗的是以下的情境:一面讓沙漏左右擺動,而且拿著線的手也同時前後擺動,則沙子畫出什麼圖形?
用圖片來說明會更清楚:如圖一(左)的兩個單擺,左邊的單擺往東西向擺,右邊的單擺往南北向擺。筆尖安裝在右邊單擺的尖端。則讓兩個單擺一起擺,右邊的單擺在南北向擺的同時,也會因為左邊單擺的影響而位移。此時筆尖畫出什麼圖形?
圖一:(左)左邊的單擺往東西向擺,右邊的單擺往南北向擺。
(右):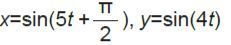
由高中物理我們知道,單擺擺動投影到地面,相當於正弦函數投影在y軸上。因此,以數學的觀點來看,這個曲線就是兩個沿著互相垂直方向的正弦振動,其合成之後軌跡。寫成參數方程式就是
其中t是參數。有一些特殊值是無趣的:當a= b = 1, 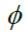 = 0 時是一條直線。當a = b = 1,
= 0 時是一條直線。當a = b = 1,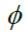 =
= 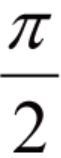 時是一個圓。但一般來說,圖形會與兩個擺的頻率有關,a ≠ b 時,畫出來的圖形相當美麗。圖一(右)就是
時是一個圓。但一般來說,圖形會與兩個擺的頻率有關,a ≠ b 時,畫出來的圖形相當美麗。圖一(右)就是
這些圖形雖然首度提出的人是Bowditch,但現在通稱為Lissajous曲線(Lissajous curve),得名自Lissajous於十九世紀中開始的詳細研究。現在它偶而會出現在某些大一微積分課本中,當作參數曲線一章中的習題。......【更多內容請閱讀科學月刊第536期】