- 精選文章
文章專區
2014-11-01規範對稱與基本粒子
539 期
Author 作者
賴昭正/前清大化學系教授。
在《科學月刊》第41卷第三期(2010年3月號)〈對稱與物理〉裡,筆者談到了對稱(symmetry)在物理定律上所扮演的角色及其重要性。在那裡,我們談到了電荷對稱(charge conjugation symmetry,即正物質與反物質之對稱,簡稱為C)、鏡像對稱(parity symmetry,即鏡像與原像之對稱,簡稱為P)、時間對稱(time reversal symmetry,即時刻正流與倒流之對稱,簡稱為T),以及座標及時刻位移(translation)之對稱。這些對稱的一個共同點是:除了易懂的電荷對稱外,它們均是作用於時空(時間與空間)上,因此不抽象,很容易用我們日常生活中所學到的經驗來體會與了解。當然,除了上面所舉之例子外,物理尚有一些其他不抽象的對稱;但在這裡,筆者想來介紹一個抽象,但卻是今日基本粒子物理(甚或整個物理)發展所不可或缺的工具:「規範對稱」(gauge symmetry)。
古典力學
在進入完全抽象的領域前,筆者擬在此先用一個眾所皆知的力學──牛頓第二運動定律──來說明規範對稱的運作與意義。我們在〈對稱與物理〉裡已探討了牛頓第二運動的對稱性,除了上面所提到之不抽象的對稱性外,難道它還有隱藏的對稱──抽象的對稱?
要了解此一抽象的對稱,我們得先將牛頓第二運動「抽象化」。十八世紀的物理學家早已知道,除了可以直接用「力」來探討物體的運動外,用「能量」的概念可能具有更深遠的意義。在這一模式裡,力可由單位距離之位能變化算出。例如在重力場裡,高度為h的力F(h):
式中U(h2) 為在高度h2時的位能,又h2 > h > h1。所以牛頓第二運動定律變成(在高深物理的研究中,根本不討論力的):
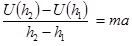 (1)
(1)
式中m為物體的質量,a為加速度。到這裡為止,我們似乎只是用另一種形式來表達牛頓第二運動定律而已!可是某些物理學家卻看到了一個新的對稱! ……【更多內容請閱讀科學月刊第539期】