- 精選文章
文章專區
2015-11-01無窮相加之美─泰勒級數
551 期
Author 作者
李武炎／曾任教於淡江大學數學系，現為《科學月刊》編輯委員。
無窮的悖論
在公元前五世紀，希臘哲學家雷諾（Zeno）曾經提出兩個很有趣的悖論（paradox，又譯詭論）。第一個悖論是敘述一個古希臘英雄阿基里斯（Achilles）與一隻烏龜賽跑的故事，他說如果阿基里斯讓烏龜先走一段距離，則阿基里斯永遠也無法超烏龜，它的論點是這樣的：當阿基里斯從點a1出發，烏龜從點b1出發，當阿基里斯到達點a2=b1時烏龜也從點b1前進到b2，當阿基里斯再到達a3=b2時烏龜也再從點b2前進到點b3。這種情況無窮延續下去，似乎烏龜永遠都在阿基里斯的前面。
布魯克．泰勒（Brook Taylor, 1685~1731）
英國人，為英國劍橋大學法學博士，但也研習數學，早年鑽研振動弦運動，成功使用數學闡述其物理效應，1715年發表泰勒級數，當時還不太引人注目，直到1772年拉格朗日（Lagrange）方才認識這個公式的重要性，並稱之為「微分計算的主要基礎」。
這個悖論牽涉到數學的一個東西，那就是無窮數列， 阿奇禮連續的位置（a1, a2, a3, ⋯⋯）與烏龜的連續位置（b1, b2, b3,⋯⋯）就是所謂的無窮數列，雖然對每一個正整數n而言，an<bn，但在極限理論中我們知道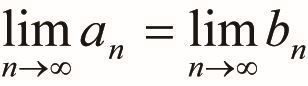
（設此數為c），也就是說在點c時，阿奇禮將趕上烏龜。另外一個悖論是與無窮級數有關。......【更多內容請閱讀科學月刊第551期】