- 專欄
文章專區
2016-06-01計程車的數學
558 期
Author 作者
游森棚／任教於臺灣師範大學數學系及空軍官校。
計程車幾何學
首先，計程車在棋盤狀的道路上穿梭，由此可以發展出一套幾何學，叫做計程車幾何學（Taxicab geometry）。假設行車道路呈棋盤狀，則計程車從正方形的一端走到另一端最短距離不是直線，而是要沿著馬路轉直角走。所以從單位正方形的一端走到另一端的計程車距離是2，而不是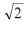
。換句話說，由P到Q只能走直或走橫。距離就是所有走過的路徑和。如果P= (x1, y1)，Q= (x2, y2)，原本我們習慣的兩點距離是：
但現在，這兩點的計程車距離是：
這個距離也稱為曼哈頓距離（因為紐約曼哈頓的道路實在非常像棋盤）。
這並不只是益智遊戲，而是有點來頭的。這是由大數學家閔可夫斯基（Hermann Minkowski, 1864~1909）首先考慮的幾何學。在高等數學上，計程車距離有正式的名稱叫做「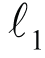
norm」，是所謂L1空間上的距離；L2空間上的距離就是我們熟悉的距離；一般的Lp空間，則屬於泛函分析（functional analysis）上的重要研究對象。
我們可以思考一下在計程車距離意義下的「單位圓」長的如何？我們要求與原點(0, 0) 的「計程車距離」為1的所有點(x, y) 所成的集合。……【更多內容請閱讀科學月刊第558期】