- 專欄
文章專區
2016-10-01小題目大道理(一)
562 期
Author 作者
游森棚/任教於臺灣師範大學數學系及空軍官校。
即將來臨的新學期,系上委託我開一門給大四的課「數學教學與解題」。這門課主要的想法是幫助未來的中學老師能夠更掌握即將要教給學生的內容,也迎接將來的教師甄試。於是這個暑假我重操舊業,讀了不少學校近年教師甄試試題。絕大部分問題真的是相當無趣,有些非常人工化且刁鑽。教師甄試如果變成解怪題比賽,是有點讓人憂心。但偶爾也有幾個珠玉題目讓人眼睛一亮。這個月的專欄來看看一個教師甄試的好問題,與求和公式有關。求和公式是不少高中師生心中的疑惑,希望這篇文章可以有一點幫助。
【問題】
若數列。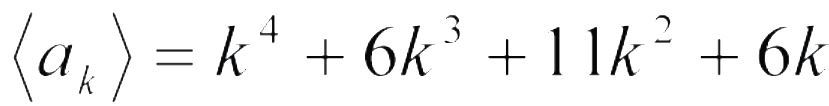 。求數列的前12項和。
。求數列的前12項和。
因為只有12項,真的把1~12全代進去再相加也許最快, 答案是104832,這應該是很多考生採取的辦法。但數學上我們還是要有一個說法,正常的程序是:
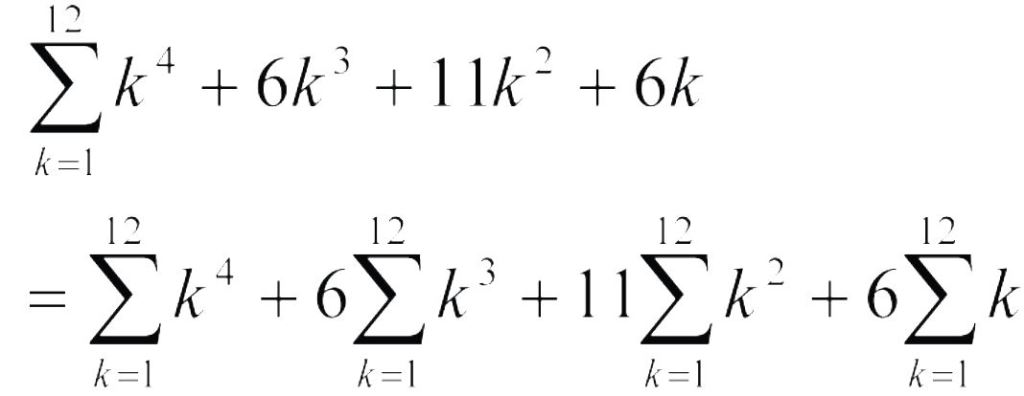
一、二、三次方的求和公式是課本內容,因此問題變成要推導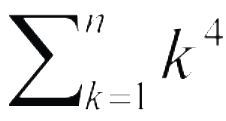 的公式。怎麼算呢?
的公式。怎麼算呢?
方法一
根據一、二、三次方的求和公式,我們有信心相信四次方求和公式應該是一個五次多項式:
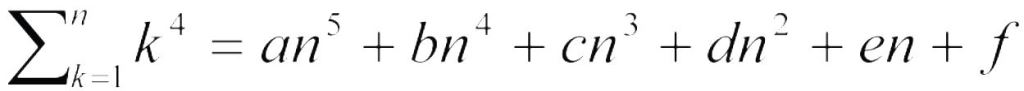 所以令 n = 1,2,3,4,5,6代進去變成一個超大的聯立方程組,就可以把(a, b, c, d, e, f)解出來。這非常笨拙,但是學生如果忘掉平方和公式,這個方法可以幫助他推導回來。
所以令 n = 1,2,3,4,5,6代進去變成一個超大的聯立方程組,就可以把(a, b, c, d, e, f)解出來。這非常笨拙,但是學生如果忘掉平方和公式,這個方法可以幫助他推導回來。
方法二