- 專欄
文章專區
2016-12-01畫鬼腳中的困難數學
564 期
Author 作者
游森棚╱任教於臺灣師範大學數學系及空軍官校。
畫鬼腳(英文也叫「Ghost leg」,日文叫「阿彌陀籤」) 是常見的抽籤方法:首先畫幾條縱線,以縱線的頂端為起點,底端為終點,終點處寫上抽籤的項目。在縱線間任意畫一些橫線,但橫線不得穿越縱線。接著每個人選一條縱線,由上方起點開始往下走,但若遇到橫線則沿著橫線走到隔壁的縱線,最後到達終點就是抽籤所抽中的項目。如圖一左的鬼腳,4往下走,經過鬼腳的走法後會抵達2。 讀者可試試看1、2、3,會分別走到 4、1、3。
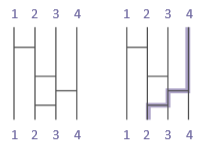
圖一我們可以把上面的這個鬼腳結果寫成:
(1, 2, 3, 4) → (4, 1, 3, 2)
於是這就引出一些觀察和相關的數學問題,在小學科展中或不少科普文章常常出現。這些分析畫鬼腳的文章絕大部分內容都差不多,無非是討論以下幾個面向:
⑴ 為什麼畫鬼腳是一對一?(即,不管橫線怎麼給,最終還是1、2、3、4各一個?)
⑵ 承上題,是否每一種結果都能出現?(即,把(4, 1, 3, 2)隨便換成一個排列,比如(3, 4, 1, 2),有辦法讓(1, 2, 3, 4) → (3, 4, 1, 2)嗎?)
⑶ 承上題,要怎麼設計出想要的結果?橫線要放在哪裡?最少要放幾條線?
⑷ 這個抽籤是公平的嗎?
在網路上可以找到許多科展或科普文章討論這些,因此以下非常簡略地說明:
問題一,鬼腳必為一對一的理由是:一條橫線就是兩縱線左右交換,因此四根縱線換來換去還是四根縱線。
問題二的答案是:可以。問題三答案是:一定可以設計出來,而最少的橫線數即數一數目標排列有多少逆序即可。 一個逆序是指一組「大……小」,比如4132有41、 43、42、32這4個。一個逆序表示相對應的兩數遲早要交換,因此由1234 → 4132至少需要4條橫線,畫法可以稍微試一下就可得到。問題二與問題三真正的背景是抽象代數中的一個結果:對稱群可以由相鄰的轉置所生成,而需要的轉置數就是逆序數。
問題四意思是,隨機畫若干條橫線,是否每個人到各頂點的機率會相同?答案為「否」。……【更多內容請閱讀科學月刊第564期】