- 專欄
文章專區
2017-01-01衛星軌道與扁圓的地球
565 期
Author 作者
金升光／任職於中央研究院天文及天文物理研究所。
克卜勒歸納出行星遵循橢圓軌道繞著太陽運行的規律。牛頓的萬有引力定律計算兩質點間隨著距離平方遞減的作用力。因此，早在兩三百年前的科學家就可以準確的預測哈雷彗星的回歸、推測海王星的存在，也預見人造衛星的誕生。克卜勒的橢圓軌道有一定的大小、形狀，長軸和軌道平面必須指向遙遠星空中固定的方向。但是，如果把這樣簡單的橢圓軌道套用在月球或是人造衛星的運行，我們很快就會發現觀測結果和克卜勒的橢圓有相當的差距。今年恰好是人造衛星60 歲的生日， 讓我們來認識人造衛星運轉的深一層原理，以及一個有點扁又不大均勻的地球所帶來的問題與研究。
低軌道衛星
從臺北開車到高雄需要耗費多少汽油？在不考慮起步和停止、沒有地球自轉、沒有摩擦力的理想條件下，慣性定律提供了一個節能減碳的選擇。扣除發射操作的成本，人造衛星繞地球基本上是不需要燃料的；但是，另一方面，衛星的速度和方向也受到物理學的限制。想像王建民投手站在玉山山頂上往水平方向投出一顆時速100公里的慢速球，這球應該會掉到山谷裡。假使這球 速能夠再快285倍以上，比每秒343公尺的音速還快， 超過每秒鐘7.9公里，且如果沒有濃密大氣的阻擋，它很有可能進入軌道成為一顆人造衛星！新世紀衛星軌道五花八門，基本原理卻沒有太大差別，讀者可參閱孫方鐸教授〈談太空飛行〉一文（《科學月刊》1980 年3月123期）及續篇。若把地球看做一顆蘋果，玉山的高度和地球的平均赤道半徑6378 公里相比，可能比削下來的蘋果皮還薄。通常，軌道距離地面高度在一、兩千公里之內的，稱為「低軌道（low Earth orbit）」。國人熟知的福衛二號、哈柏太空望遠鏡、國際太空站等等，都屬於此類衛星。它們環繞地球的軌道半徑大致和地球半徑相去不遠，只要1.5~2小時左右就可以繞地球一圈。
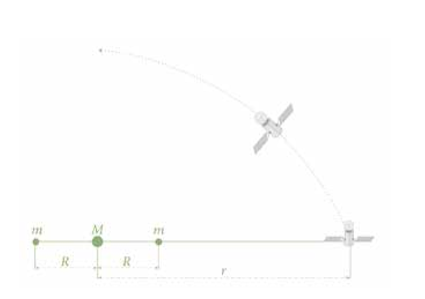圖一：非球對稱質量分布的一個簡單範例。
低軌道衛星不像同步衛星可以持續連繫或監測同一個城市或地區，運用起來有些限制。但是低軌道的發射、通訊、維護成本較低，是太空工業不可忽視的選項。對於衛星發射和基地相關問題有興趣的讀者請參閱張以棣教授〈人造衛星是怎樣發射的？〉（《科學月刊》1990年 9 月 249期）與〈衛星發射基地巡禮〉（《科學月刊》1991年6月258 期）的介紹。軌道接近地表的衛星運行和操作會受到大氣層、地球形狀與質量分布、地球磁場、甚至於月球等鄰近天體的影響，軌道形狀和方向因而偏離克卜勒的橢圓，量測通訊也可能有些特別的干擾或阻礙。我們可透過如圖一的簡單模型來說明形狀與質量分布的問題。首先，在同一直線上質量分別為m、M、 m對稱分布的三個質點，對於直線遠端一點衛星（和 M相距為r）的萬有引力並不等於某一個質量M+2m的質點在同樣距離r處的所產生的引力。也就是說：
上式中的G是牛頓的萬有引力常數，衛星質量省略。M與 m就像地球與其分布不大對稱的質量。另一方面，若衛星位置不與三質點共線，和這直線有段距離，同時衛星本身質量和M、m相比不可忽略（譬如像月球與潮 汐），可以想見衛星的運動和地球的旋轉也會相互影響。
重力場解析
地球實際上的質量分布很複雜，有山川、海洋，還有不同的岩石、礦物、板塊、冰河以及更深層的地函等結構。想像中，計算地表的重力或是人造衛星所受的力需要把所有質點產生的引力加起來，可以透過積分或現代電腦科技來達成。但是，沒有人真正知道準確的質量分布，我們只能從各種測量的結果加上理論來推估。力是一個向量，分析時不如更單純的重力位（gravitational potential, GM/r）好用。重力位可以看作是質量M 的質點對於距離r的單位質量質點所產生的重力位能。利用牛頓、萊布尼茲所發明的微積分，可證明球對稱分布的質量所產生的萬有引力相當於將所有質量集中在球心所產生的引力。圖一的簡單模型並不具有球對稱性。
許多天體和地球類似，都擁有接近球對稱的外形。……【更多內容請閱讀科學月刊第565期】