文章專區

資料長什麼樣子？

要描繪資料的樣貌，我們可以從中心點在哪以及分布狀況如何，這兩個層面來回答。

為了方便讓讀者了解，這裡我們用「數感實驗室（Numeracy Lab）」在 2017 年初所做的「孝敬父母的紅包大調查」，以受訪者的年收入與年紀來討論「給父母的紅包金額」的有趣分析當例子。討論之前，我們必須先提醒讀者，「民意調查是怎麼做的？」對於統計分析結果的正確性影響很大，譬如誰是「紅包大調查」受訪者？由於這個調查是直接發布在臉書的粉絲頁，主動填寫問卷的人除了本身就具有數感實驗室的「粉絲」特徵（可能是喜歡數學的人、重視小孩教育的父母、喜歡數感小編的寫作風格等）之外，可能還具有某些特質，比如說也許是覺得自己包的比較多或是收入比較高的人傾向願意填寫，造成最後的結果可能會有略為高估的情形。簡單來說，這些自願送上門來的受訪者或是在路上隨意發問卷來的受訪者，都屬於非隨機抽樣，因為不知道他們與我們實際感興趣的那個群體所有人（母體）的差異，因此只能針對被調查的這群人進行描述性的說明，而不能進行推論。這個資料庫大家不會太認真討論正確性，但是可當作一個例子讓大家了解如何解讀資料。

中心點在哪？

「紅包大調查」由於是網路自填問卷，主動填答的受訪者只能代表他們自己，而由資料中我們可以知道有效的259個受訪者的性別、年齡、家庭收入和雙親紅包總和，並針對這些受訪者來討論紅包金額平均多少？是否大家都差不多、還是有些人特別多或特別少？這時候，「平均數」就是一個很方便檢視資料樣態的工具。

平均數大家都相當的熟悉，是所有觀察值的總和除以個案數，也可以被視為一組資料的中心點。如紅包區間圖所示，我們可以很快速的知道這259個受訪者包給父母的紅包平均金額為17000元，大多數集中在0~2萬元之間。另一個與中心點相關的概念是中位數，也就是將所有受訪者依紅包金額高低排序後，最中間那一位的金額，在這筆資料中第130位受訪者的金額是12000元。由平均值與中位數的相對位置來看，可以發現平均值較易受到極端值，也就是最高金額12萬的影響，導致大部分受訪者所包的紅包金額低於平均值。這例子也顯示雖然由平均數來看中心點相當便利，卻不見得每一次都是最適合的工具。政府單位公布的薪資調查資料也有相似的情形，公布的平均薪資與民眾感受有相當大的落差，而相對較低的中位數反而更貼近民眾所感受到的薪資水平，這反映了我國薪資的整體分布實際上是往低薪的一端傾斜，在這種情況下以中位數來看薪資會比平均數更有意義。

資料的分布狀況？

在知道資料的中心點後，另一個要問的是：資料的分布呈現什麼樣子？若用於民眾態度的調查，就是民意是集中的還是分散的呢？這個問題可以交給標準差（standard deviation）來回答。標準差是指資料中各點與中心點的「標準距離」，以定義來說，是各點與中心點的距離（相減後的差）平方後累加起來取平均數，再開根號還原。標準差反映的是資料中各點之間的離散程度，當資料越集中，各點與中心點的距離越近，標準差越小，反之，資料越分散，各點與中心點的距離越遠，標準差就越大。

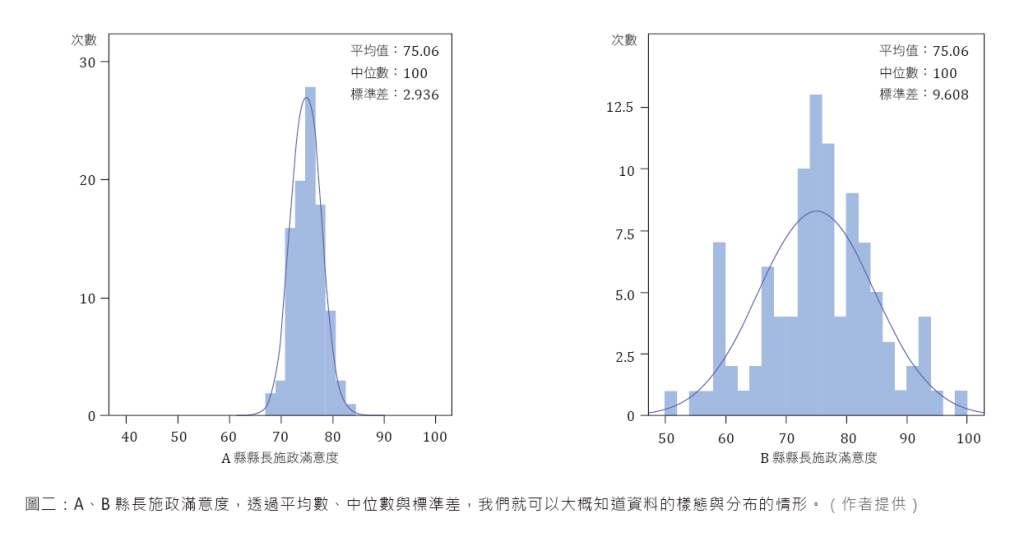
在檢視資料時，了解離散程度非常重要，原因在於：擁有同樣中心點的兩筆資料，可能有完全不同的分布情形。當民調資料只看平均數而不管離散程度時，很容易做出錯誤的解讀。以縣市首長的施政滿意度調查為例，若各請100位受訪者以0~100來表示對縣市首長的施政滿意程度，假設A、B兩縣縣長的滿意度平均數皆為75.06，但A縣是大多數受訪者的滿意度集中在75上下，則標準差小（2.936），而B縣受訪者的滿意度分散於50~100之間，則標準差大（9.608）。兩縣接受調查的民眾看似都對縣長施政傾向滿意，但由離散程度來看，B縣必須特別注意極端意見的民眾，避免在某些情況下出現高強度的反彈，造成施政的困難。

樣本與母體長的不一樣怎麼辦？我們要怎麼推論？

只要不是普查，抽取出來的樣本一定會與你感興趣的母體之間有落差。因此，在解讀時必須特別注意「抽樣誤差」的存在。若是非機率抽樣，我們不清楚這些人的特性與母體之間的落差，因此僅能就有回答的這些人做結果的說明與闡述，不能推論到所有的人。若是再進一步推論，所做出來的詮釋一點根據也沒有，萬萬不可相信。

我們經常在媒體上看到很嚇人的民調數字，比如說：「一例一休後，3成上班族薪資縮水一成！」。這些數字怎麼來的？真的可以這樣子推估嗎？以104人力銀行的資訊科技針對求職會員進行「一例一休影響」問卷調查為例，這些求職會員通常具有某種同質性，也許是對於現在的薪資不滿想轉換跑道，也許是剛開始找工作的新鮮人，有著各種的可能性，總之並非隨機抽樣，這些同質性可能造成調查結果的偏誤。因此調查結果「已有30%上班族因公司管控加班、少賺加班費，導致實質薪水變少，平均減少幅度11.3%」，只能說明這群受訪者的情形，並不適合用來推估所有臺灣的上班族。

即便是隨機抽樣，僅用少數抽取到的樣本觀察值來推估母體被稱為「點估計」，是不可能精準的。就像是在校門口隨意抽取50個學生量完身高算出平均（樣本平均數）後，就想要命中這間學校全體學生的平均身高（母體平均數），是幾乎不可能的事。......【更多內容請閱讀科學月刊第571期】