- 專欄
文章專區
2020-01-01教科書外的數學─ 整數數列線上大全OEIS
601 期
Author 作者
林家妤 Shark Lin 因為數學成為斜槓青年,進行數學藝術創作、策展、採訪、寫作與創意教學,特別喜愛跨領域的題材與合作。
有些人喜歡蒐集化石,有的人是益智玩具迷,那你知道有人專門蒐集整數數列嗎?
整數數列的收集與紀錄
整數數列,是指一個由整數形成的數列,例如知名的費氏數列(0, 1, 1, 1, 2, 3, 5, 8....),由0和1開始,之後則是由前面的兩數相加得出。而整數數列線上大全,則是專門蒐集整數數列的網站,由數學家斯洛恩在1996年設置建立,因此也簡稱為Sloane’ s。
斯洛恩於1939年出生於英國威爾斯(Wales),小時候移民至澳洲。大學時期以五年時間完成雙修數學與電機工程的學位,1965年就讀美國康乃爾大學(Cornell University)研究生時期開始蒐集整數數列,當時他把蒐集到的數列寫在檔案卡上,即使後來到貝爾實驗室(Nokia Bell Labs)與AT&T工作時仍持續蒐集整數數列。
1996年,整數數列的數量達到一萬條,因此斯洛恩決定用線上的方式完整記錄整數數列,直到去(2019)年6月,OEIS已收集超過32萬個數列,是世界上同樣類型的資料庫中規模最大的。過去一年,網站新增了12000條數列,並且獲得8000次引用。
每天都有數學家把新的數列寄給斯洛恩與其團隊,而每個月將近千萬點擊率,高到一般科普網站都追不到車尾燈。然而,點進OEIS的網站一看,會發現介面樸實無華,卻仍能夠對數學界有如此深遠的影響,歸功於斯洛恩與背後眾多主編與副主編審核各方提交的新數列。
新數列的產生使得OEIS集合許多有趣的數學問題,這些發想通常是從趣味數學的社群而來。事實上,OEIS的特色即是整合專業數學家與業餘數學家,讓全球的數學愛好者能夠一同在此交流。
美國羅格斯大學(Rutgers, The State University of New Jersey)的齊爾伯格(Doron Zeilberger)教授認為斯洛恩是在世的數學家之中最有影響力的一位,雖然他並沒有成功證明費馬最後定理(Fermat’s Last Theorem)或龐加萊猜想(Conjecture de Poincaré),然而,今日OEIS對於數學研究的影響力遠超過任何一位在世的數學家。
OEIS上的數列
那麼,要如何玩OEIS呢?一開始可以用關鍵字及鍵入部分數列的方式搜尋到完整條目,像是費氏數列可以用Fibonacci(費波那契)搜到條目A000045,如果一開始不知道要從哪邊入坑,OEIS上也有預設的數列可供入門者一鍵搜尋。
每一個條目都列出了該數列的前幾項(約30~40項)、關鍵字、數學動機、文獻連結與相關圖形,甚至可以把數字當作八度音階的音符,再模擬各種不同樂器形成音樂,讓人以全新的方式感受數列。
今(2020)年已經80歲的斯洛恩,除了幾乎每天都會提交1~2則新數列,還經常活躍於YouTube與Podcast,他也曾經分享過幾個充滿趣味的數列,在此就列舉幾個例子讓大家看看有別於教科書的數學奧妙:
數列A133058:Fly straight,damn it!
這個數列的圖形讓斯洛恩想到《阿凡達》(Avatar)男主角傑克第一次駕馭靈鳥(banshee)卻失控的情景,因此斯洛恩稱它為「Fly straight,damn it !」,現在,就讓我們一步步來看看A133058生成的奇妙圖形。
首先,先定義A133058 的前兩項為1,那第三項(n=2)的數值要如何計算呢?
規則一:
如果n與a(n-1)之間沒有公因數,那麼,下一項則a(n)= a(n-1)+n+1,如圖一。
在這個例子中,n=2 時n與a(1)沒有公因數,因此,a(2)=1+2+1=4。下一項n=3時,發現3與4沒有公因數,因此a(3)=4+3+1=8,如下:
規則二:
如果這兩項最大公因數(gcd)大於1,下一項的數值就是前一項的數值除以a(n-1)與n 的最大公因數,也就是a(n)= a(n-1)∕gcd(n, a(n-1))。接著n=4 時,發現n與a(3)有公因數,因此a(4)=8/4=2,如下:
若用這兩項規則產生後面的數列(圖二),則會得到以下數列,如下:
按照這樣的規則,則會生成圖三的數列與圖形,神奇的是,從第638項以後,圖形會收斂成三條直線,就像是在空中飛行一般。
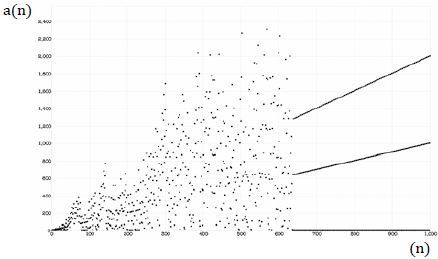
圖三
接著,再來看看第638項前後到底發生了什麼事,讓原本散佈的圖形收斂成三條直線?首先我們可以觀察到,第638項的值是1,接著依照前面的規則計算出後面像次的數值,如下:
為了以數學解析638項之後的數字,在此以代數2m表示項次,並且計算後續的項與數值以便觀察。按照先前的兩條規則,可以計算出第2m+1到第2m+11的項。仔細觀察這表,可以把每四個數字分成一組,便會發現規律了!
從第638項後的數列只有三種類型的組成:整數1和2(姑且稱為數列A1與A2);2m+3、2m+7、2m+11等前後差4的數字(數列B);及4m+6、4m+14、4m+22等前後差8的數字(數列C),如下表。
這樣就可以解釋為什麼圖形最後會收斂成3條線,圖三最下面那條看似只有一個數字的直線其實是數列A1與A2;而中間那條斜率沒那麼大的線,則是數列B構成;同樣的道理,最上方那條斜率最大的線,則包括數列C中4m+6、4m+14、4m+22等數字。
這個奇怪的圖形就像是阿凡達男主角傑克的學習歷程,一開始傑克還沒辦法駕馭靈鳥到處橫衝直撞,過一陣子終於掌握到技巧便可以順利地往前直飛了,而這圖形正是數學展現出來的魔術,屬於大自然的奧秘。
原來人類偏好會影響數字的受歡迎程度:斯洛恩縫隙
OEIS龐大的資料庫本身也成為數學家好奇與研究的對象,例如每一個數字的相對重要性,如果一個數字可以被越多的規則描述,表示這數字可能越有趣,在OEIS裡出現的頻率也就更高。因此,數學家將OEIS資料庫數字n出現的次數N繪製成圖四,從圖中可以看到數字從小到大,出現次數呈現遞減的趨勢。
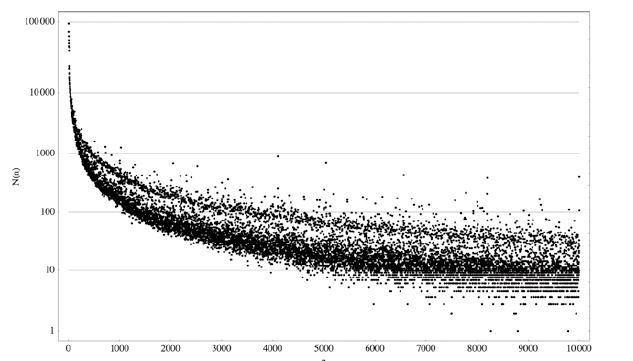 圖四
圖四
從圖中可以發現,中間有著明顯的一條縫,這條縫被稱為斯洛恩縫隙(Sloane’s gap),將不同的數字分為較為受歡迎的上層及較不普遍的下層。上層的數字包括質數、費氏數列、
95的平方數、2的次方數加1或減1(2n+1 或2n-1)、有很多因數的數字及在十進位系統中看起來有趣或順眼的數字,像是1111、2222或3333等。而其他沒有這些特性的數字,大多在下層。
斯洛恩縫隙道出一個驚人事實,原來每個數字並非生而均等,其重要性會強烈受到人類偏好也就是文化的影響。看似全然理性的數字,經過人類的研究之下,竟然會有受歡迎程度之分,這也告訴人們,原來人類文明和數字息息相關。
閱讀別人發展的數列有點無趣嗎?其實,你也可以自創數列投稿,只要英文與程式能力達到一定水準,就有機會讓自己的數列被OEIS蒐藏,和世界分享數學的規律與驚奇。
延伸閱讀
1. OEIS:http://oeis.org/。
2. Alex Bellos, Neil Sloane: the man who loved only integer sequences, The Guardian, 2014/10/7.
3. Gauvrit, Delahaye and Zenil, Sloane's Gap: Do Mathematical and Social Factors Explain the Distribution of Numbers in the OEIS ?, Journal of Humanistic Mathematics, 2011.