- 封面故事
- 2016年
- 564期－2016諾貝爾獎特別報導（12月號）
文章專區
2016-12-01拓樸理論 提供物質新觀點
564 期
Author 作者
張泰榕；曾郁欽
.JPG) |
索利斯（David J. Thouless, 1934 ～）
國籍：英國
現任：華盛頓大學榮譽教授
研究領域：凝聚體物理學 |
.JPG) |
科斯特利茨（J. Michael Kosterlitz, 1942 ～）
國籍：英國、美國
現任：布朗大學物理學教授
研究領域：凝聚體物理學 |
.JPG) |
霍爾丹（F. Duncan M. Haldane, 1951 ～）
國籍：英國、美國
現任：普林斯頓大學物理學系教授
研究領域：凝聚體物理學 |
2016 年的諾貝爾物理獎頒給了三位理論物理學家，美國華盛頓大學的戴維· 索利斯（David J. Thouless）、美國普林斯頓大學的鄧肯·霍爾丹（F. Duncan M. Haldane）以及美國布朗大學的約翰·科斯特利茨（J. Michael Kosterlitz）。得獎理由為「拓樸相變（topological phase transition) 與物質拓樸相的理論發現」。
故事開始⋯⋯
我們生活周遭充斥著各種「物質」，例如金屬、絕緣體和半導體等，現今的科技成就，大部分可說是奠基於對物質的深入了解。另一方面，科技與科學的進步建立於典範的轉移，如愛因斯坦的相對論開闢了一個異於牛頓力學的全新視野，讓我們能從完全不同的面向去認識宇宙。今年獲獎的三位大師均來自英國，運用高超的數學技巧及敏銳的物理直覺，以「拓樸（topology）」這全新的觀點來理解物質，替人類對物質知識的建立開闢了一條全新的道路。
物質態與相變
在介紹這些讓人興奮的非凡研究之前，讓我們翻開自然課本，打開塵封已久的記憶，重新回顧一下我們對物
質的了解。如果沒有把課堂知識全部還給理化老師，應該可以回想起物質可分為三態：氣態、液態與固態。這三種物質態各自表現出來的物理特性有著極大的差異，例如冰很硬，被砸到會很痛；水會弄溼衣服，涼涼的。三態之間可以互相轉變，例如水可以變成冰（液態變固態），科學家稱這種轉變為相變（phase transition）。相變的研究在科學領域中佔有至關重要的地位，因為相變的發生代表著物
質態產生劇烈的變化。通曉其中的奧秘，無論對於自然界本質的了解或是未來科技上的應用，都有著無可忽視的巨大潛力。
科學家如何分辨相變？
1980 年以前，物理學家會以「對稱性」來對物質態進行分類，當對稱性發生變化同時即反映了物質的相變。為了顯示其專業性，我們給了這種分類方法一個專有名詞：「對稱性破缺（symmetry breaking）」。什麼是對稱性呢？如圖一，一個正方形對其中心旋轉90 度後外觀上看來與旋轉前完全相同，你無法分辨是否有做過旋轉，但旋轉70 度則不同，我們稱正方形具有90 度旋轉的對稱性。如果是圓，則是旋轉任意角度皆不變，因此圓的對稱性比正方形來的高。
圖一：正方形，對其中心旋轉90 度後外觀上看來與旋轉前完全相同，無法分辨是否有做過旋轉，但旋轉70 度則不同，我們稱正方形具有90 度旋轉的對稱性。正圓，則是旋轉任意角度皆不變。下圖，原子在液體中可隨意排列，因此液體可以任意改變形狀，無論從哪個角度看都是相同的。但固體則不然，當液態轉變成固態的同時物體中的原子排列會發生非常劇烈的變化，從雜亂無章變成如軍隊般的排排站好，此時你無法任意改變物體外型，且從不同角度觀看皆會看到不同幾何形狀。
現在我們將這觀念套用上對稱性破缺，來看一個相變的實際例子。當我們對液體降低溫度後，液體會凝固變成固體，發生液態– 固態相變。
液體因為內在原子任意分佈，可以輕易改變外觀形狀，無論從哪個角度看都是相同的。但固體則不然，當液態轉變成固態的同時，物質內部的原子排列會發生非常劇烈的變化，從雜亂無章變成如軍隊般的排排站好，此時你無法輕易地改變物體外型，且從不同角度觀看皆會看到不同幾何形狀。和液態相比，固態的對稱性明顯低了很多，我們以這簡單的例子說明對稱性變化即對應物質相變的發生。
此時好奇的你∕妳一定會想問，是不是所有自然界的相變都可以用對稱性破缺來描述？有沒有例外？另外如果我們是居住在一維或二維世界的生物，那對稱性破缺的概念還能不能用？還會不會有相變？沒錯！解答這些問題正是這三位物理獎得主最重要的貢獻，他們的研究工作讓我們對相變的認識有了全新的視野。
問題來了！
早期的研究發現，一維或二維系統中只要溫度高於絕對零度（-273.15°C），哪怕只比絕對零度高出0.1° C，有序排列的狀態就會被無可忽視的熱擾動（thermal fluctuation）所摧毀而無法產生對稱性破缺。根據先前提過的「對稱性改變等於物質發生相變」的邏輯思路來推想，會得出此種情況下無法發生相變的結論。但大自然真的是如此嗎？
突破性的開端，KT 相變
為了徹底理解二維相變問題，1970年左右索利斯與科斯特利茨提出一個理論模型，他們假設在二維平面上有無數個小磁鐵（精確來說是二維向量場）。如果依照傳統對稱性相變理論，因為沒有對稱性破缺，這些小磁鐵應該會隨意的各自指向不同方向（可以想成一堆沒受地磁影響而亂轉的指北針）。然而他們的模型卻顯示出完全異於直覺的結果。這些小磁鐵在慢慢增加溫度時會產生成對的渦流（vortex），一個向左轉、另一個向右轉，兩兩成對，無一例外（圖二左）。如果繼續升溫，當溫度高過一定程度後，這些渦流會好像情侶分手一般不再成對出現，而喜歡單獨出現，形成各自的渦流（圖二右）。在這變化途中並不涉及對稱性變化，但小磁鐵卻表現出兩種不同的集體行為（成對渦流或單一渦流），證實了相變的發生。這是人們在相變的研究中第一次超越了對稱性的限制。這種相變被稱為「KT 相變（KT phase transition）」。索利斯與科斯特利茨之後理解到這種奇異的二維相變行為需要拋棄幾何的包袱，引入「拓樸」的概念才能有效的解釋。
拓樸非常重要！
這邊稍微離題來聊一下「拓樸」。「幾何」是我們求學過程中較為熟悉的，就是圓形、三角形、正方形等不同圖型。討厭數學的同學可能會想起每次考試都要絞盡腦汁計算不同形狀的邊長與夾角等不堪回首的記憶。比起幾何，拓樸對我們來說就比較陌生。
拓樸正好和幾何相反，在拓樸世界中我們不需去理會物體的外在形狀，只要去留意上面有幾個「洞」，洞的數目相同代表相同的拓樸，洞的數目不同則代表不同的拓樸（圖三左）。在不改變洞的數目的情況下，如果一個物體能連續變化到另一個物體，那這兩個物體的拓樸就是相同的。最耳熟能詳的例子：一個有把手的咖啡杯和一個甜甜圈的拓樸是相同的，但和具有兩洞的眼鏡是不同的。甜甜圈能連續變化成有把手的咖啡杯，但除非你在甜甜圈上多開一個洞，不然它絕對無法被你扭成眼鏡。
KT 的一小步，人類的一大步
在KT 的模型中，我們可以把渦流類比為大海中的漩渦，如同漩渦像海上的洞，渦流在KT 模型中就是無數小磁鐵海上面的洞，這恰巧對應到數學中的拓樸態。這種相關性之後被廣泛應用到如超流體（superfluid）相變等各個物理分支中。拓樸這原本和物理八竿子打不著關係的數學理論，在大師們的神來之筆下與物理現象有了巧妙的連結。
圖二：KT 相變。箭頭為磁矩方向，左圖渦流成對出現，在升溫經過相變之後則單獨出現（右圖）。這類相變並不涉及對稱性改變，需引入拓樸的概念才能有效的解釋。（修改自Nobel Prize）
.JPG)
圖三：上圖表示各種不同拓樸下的變化過程，每條同顏色線段內的拓樸都相同，不同顏色線段的拓樸則不同。例如橘線段區域內的物體都沒洞，藍色有一個洞，紅色有兩個洞。下圖是量子霍爾效應電導的拓樸示意圖描述。無電導在拓樸圖像中就是沒有洞（如圖中的杯子），兩倍電導是兩個洞（如圖中的眼鏡），以此類推。（修改自Nobel Prize）
在這之後索利斯持續對物理中的拓樸態進行更深入的研究，最著名的工作是以拓樸觀點來理解量子霍爾效應（Quantum Hall effect）。古典上只要外加一個電場驅動電子即可形成電流，不同材料對同樣大小的電場所產生的電流大小都不同，這種天生的內在性質稱為電導。然而科學家發現，如果對一個二維系統（例如很薄的半導體材料）在很低溫時額外加上垂直於表面的強磁場（圖四左），這時電導會隨著磁場強度增加呈現2~4倍等整數倍變化，不會因材料不同而改變。數學上我們可以寫成：電導σ=c．N，其中c 為常數，且N=1,2,3,…。索利斯發現上述公式的N恰巧可以對應到拓樸學的「洞」，例如兩倍電導（N=2）表示有2 個洞、三倍電導（N=3）則有3 個洞，以此類推。拓樸又不可思議的再一次的和物理有了巧妙的連結（圖三右）。
量子霍爾效應的應用
量子霍爾效應所產生的量子電流不會因材料內部雜質散射而產生電阻（圖四右），這種零電阻的非耗散電流不但能有效提高電子元件效率，更能節省能源消耗，充滿了未來的應用前景。然而外加磁場因設備大小的限制，無法簡單的製成奈米等級元件，此外持續外加強力磁場對現有技術和成本上都不易達成，這些不利因素大大限制了量子霍爾效應的應用可能性。看似束手無策的難題，霍爾丹飛躍性的物理直覺在這個議題上提出了開創性的貢獻。
圖四：左圖為一個二維系統，例如很薄的半導體材料在很低溫時外加上垂直於表面的強磁場，這時電導會隨著磁場強度增加呈現2~4 倍等整數倍變化，不會因材料不同而改變。右圖是在一維世界中，電子只有向左或向右兩條路（圖右上兩條紅線），這兩條路和雜質之間的隨機散射即是電阻成因。如果我們能將這兩條路拉開，例如右下圖，向左電子遇到雜質，但因為沒有向右的路可以回頭，此時電子會像沒看到雜質般的繞過去而不產生電阻。這種條件雖然在一般材料很難達成，但量子霍爾效應卻能神奇的實現此現象。量子霍爾效應中電流不會因電阻而產生熱能消耗，比起傳統電子元件，更能有效提高效率與節省能源消耗。
霍爾丹在80 年代問了一個問題：「量子霍爾效應有沒有可能在無外加磁場時產生？」他為了解決此問題而提出了一個理論模型，之後大家便以他的姓氏命名這個模型――「霍爾丹模型（Haldane model）」。在霍爾丹模型中，霍爾丹假設原子（晶格）排成二維的蜂巢狀結構（圖五上），電子在原子間跳躍，藉由特殊的跳躍路徑（如箭頭所示）來模擬外加磁場的效果，以此生成整數的量子霍爾電導。這個想法非常漂亮，但不幸的是霍爾丹模型因過於特殊，不容易在實際材料中實現，在當時（80 年代）因為材料科學與技術尚未成熟，霍爾丹的研究並沒有引起太大的迴響。然而近10 年，物理學家們發現霍爾丹模型可以做更進一步的推廣，造就數個與拓樸相關的子領域如雨後春筍般產生，例如近幾年爆紅的拓樸絕緣體（topological insulator）、拓樸半金屬（topological semimetal）、拓樸超導體（topological superconductor）等，這些新理論中基本概念的源頭皆源自於霍爾丹模型。另一方面，無外加磁場的量子霍爾效應終於在2013 年左右被實驗證實，現被稱為量子奇異霍爾效應（Quantum anomalous Hall effect）。
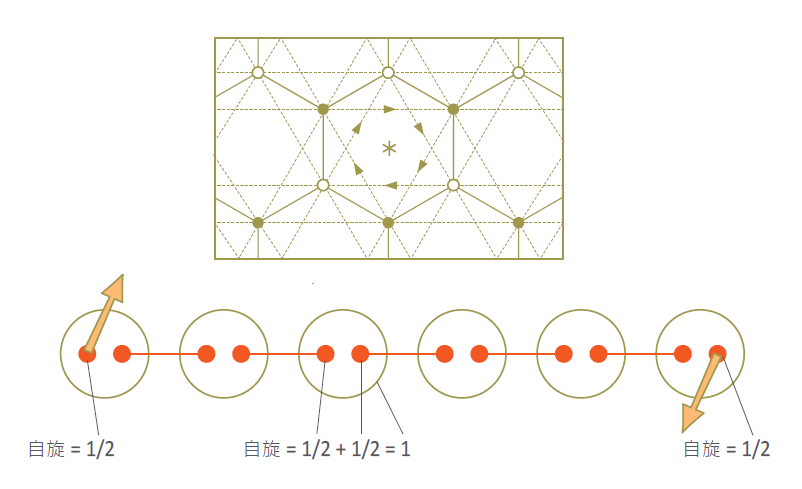
圖五：上圖，霍爾丹模型。原子排成二維的蜂巢狀結構，電子在原子間跳躍，實線表示正常的電子跳躍，虛線箭頭表示電子特殊的跳躍路徑，藉此模擬外加磁場的效果而產生量子霍爾效應。下圖，自旋大小為1 的一維磁性鏈模型。在自旋整數的情況下一維磁鏈（紅點）會具有拓樸性質，孤立的半整數磁矩在磁鏈的兩個端點（橘色箭頭），這是可直接觀測的物理量。
霍爾丹把拓樸帶入量子力學
霍爾丹對於拓樸的貢獻不只如此，80 年代他同時專注於一維量子磁性的研究。量子力學發展之後人們已經知道在量子效應的作用下，自旋磁矩只會呈現整數（S=1,2,3…）與半整數（S=1/2,3/2,5/2…） 兩類。如果將小磁鐵（精確來說是自旋）如同鎖鏈般筆直地排列在一起，霍爾丹發現不同磁矩大小排成的磁性鏈會呈現兩種截然不同的特性。在磁矩大小為奇整數時，一維磁性鏈會帶有拓樸性質，其他的磁矩大小所排成的磁性鏈
則沒有拓樸性質。一般來說實驗沒有辦法直接測量系統的拓樸性質，但在霍爾丹的先驅帶領下，人們發現一維磁性模型中，拓樸相會產生孤立且自由的半整數磁矩在磁鏈的兩個端點（圖五下），這是可以直接觀測的物理量。實驗也迅速的在3 年後於三氯化銫鎳（CsNiCl3）材料及其他鎳的化合物中驗證了霍爾丹的理論預測。
霍爾丹對物理研究的熱愛毫無保留，筆者聽朋友轉述，某次他向霍爾丹請教物理問題，霍爾丹邊吃沙拉邊在黑板上推導公式。討論到一半時，看到他滿手的粉筆灰，竟然隨意抹在身上，開始用手吃起沙拉來，那個物理人的真性情，一覽無遺啊！
量子電腦：拓樸，不可或缺
透過三位大師所打下的基礎與後續眾多研究者們的努力，拓樸的概念現已深化到物理的各個分支中，各種維度的拓樸理論與拓樸分類都相繼被提出。近十年來，實驗學家也在越來越多的材料中發現物質的拓樸態，甚至還能進一步的以人為方式控制量子拓樸相變。接下來的時間，科學家們在繼續深入探討拓樸基本理論的同時也預計朝拓樸應用方面開始邁進，像是大家期盼已久的量子電腦（科幻類電影的基本橋段）。雖然量子電腦具有量子力學天生的特性，靠著量子態傳遞量子訊息，預期其計算速度是傳統電腦難以望其項背，但因現有材料所生成的量子態極為脆弱，容易受外界雜訊干擾而被消滅，要維持大量的量子單元進行運算非常困難，這方面的研究進展一直受到阻礙。
拓樸的出現可說是替量子電腦的實現帶來了一道曙光，科學家發現如能將量子訊息分配到拓樸超導體中的「馬約拉納費米子（Majorana Fermion）」上，因這種費米子天生具有拓樸特性，外界的雜訊干擾只會改變其量子態的外型而無法改變量子態的拓樸性質（也就是量子態上「洞」的數量），因此這種量子態非常穩定，可作為運算單元來實現量子電腦。近年來拓樸應用的相關研究正如火如荼的進行，科學家之間的競爭如戰爭般的互不相讓，人人都想脫穎而出。雖然可能還言之過早，但也許不久的未來，拓樸會離開學術象牙塔，走入社會，我們的生活圈將自然地充滿著「拓樸」。讓我們一起拭目以待吧！