- 專欄
文章專區
2017-11-01高度是什麼?
575 期
Author 作者
史天元/任職於國立交通大學防災與 水環境研究中心,專長是測量工程、遙感探測、地理資訊系統。
「前、後、左、右」或「東、南、西、北」,所描述的是一個二維的世界。然而,我們所處在的空間有垂直維度,並非總是可以用「平面」理解,最常見的是球體面上的經緯度。 我們也常用全球導航衛星系統(如GPS)定位,可獲得是「幾 何高」。垂直維度與生活息息相關,故其量度必須有物理的性質,而物理性質則與位能有關,例如灌溉、排水及水力發電時,需要水力坡降的計算。
幾何、物理、高
「地球的形狀為何?」在過去是個有趣問題。古希臘畢達哥 拉斯(Pythagoras)在公元前6世紀提出地球為球形的概念, 但是他的想法是源自於「球形」為完美圖形,而不是基於對 實際現象的了解。公元8世紀中國唐代太史監南宮說,根據一行制《大衍曆》要求,在今河南省進行天文大地測量。測量結果為子午線上緯度差一度的地面距離為132公里,這是 世界上第一次實地弧度測量。此後的1000年,弧度測量陸 續的在東西文明中進行。公元17世紀末,英國的牛頓(Isaac Newton)和荷蘭的惠更斯(Christiaan Huygens)根據地球 自轉所產生之離心力,推論出地球是兩極略扁的橢球。18世 紀中葉,法國科學院在北歐接近極區的拉布蘭(Lapland) 及南美接近赤道的厄瓜多(Ecuador)進行弧度測量,證實 了地扁說。在這一階段,「地球的形狀」是以幾何性質的橢球描述,雖然這個形狀有著離心力的物理背景。
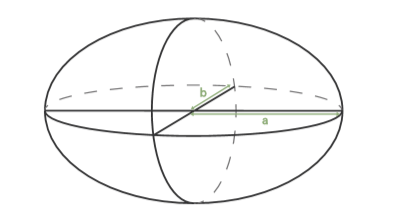
在測量上,對於表現「平面」位置而言,一個幾何曲面是十分方便與有效的。因此,「參考橢球體」是「測量基準」中的形狀基準,選擇「參考橢球體」的原則,是選用最貼 合地球實際形狀的。現行「1997臺灣大地基準(TWD97)」 採用1980年國際大地測量學與地球物理學協會公布之參考 橢球體(GRS80), 如圖一所示,地球的橢球參數為:長半 徑a=6378137 公尺、短半徑b=6356752 公尺。圖一為了示意,看起來很誇張,實際上長短半徑很接近,人眼是看不出地球有點偏橢圓的。測量專家喜歡另外用「扁率」來 描述橢圓,扁率是長半徑a與短半徑b差值除上長半徑的 比值,而地球模型的扁率f=1/298.257222101。以此可看 出,測量專家對精準度是如此的苛求。
「幾何高(Geometric Height)」是由橢球定義。圖二中 的「高」其實有不同定義。定義了橢球體,也就定義了垂 直於橢球體的「橢球高(Ellipsoidal Height)」。如圖二中R點之橢球高hr,其為橢球面至地表點之法線距離。因 為是單純的幾何量,故又稱「幾何高」。橢球高透過全球導航衛星系統的定位,可以方便、經濟的測定。在當今全球變遷的觀測中,橢球高有定義明確、施測容易的優點,故而成為監測的主要工具。
回到人類生活的物理面向,「高」有著「力」的涵意,由此定義「正高(Orthometric Height)」。「正高」以「大地水準面 (Geoid)」為其參考面,要了解「正高」與「幾 何高」的區別,我們需要先了解「大地水準面」。依據定義,「大地水準面」為通過地球海洋在靜止時的一個面。海面高因當地潮汐隨時間而異,通常以一個選定驗潮站長時觀測得平均海水面定義,故正高基準需與潮位系統連接。 臺灣現行的正高系統的零點定義,根據「2001臺灣高程基準(TaiWan Vertical Datum 2001, TWVD 2001)」,以 1990 年1月1日標準大氣環境情況下,基隆潮位站1957 年至1991年之潮汐平均海水面為零點。
如圖二所示,「橢球面」與「大地水準面」是不同的,「正高」的定義是所量度的點與該點到「大地水準面」法線方向的距離。譬如,地表點P、Q到大地水準面之鉛錘線長度 (Hp、Hq), 若該點到大地水準面之鉛錘線為直線,則「正 高」約略為該地表點至大地水準面之距離。而「高程差」指的是地形面上的兩地面點之高程。
在測量作業過程中,兩點位置放水準尺,平行當地重力方向,儀器站置放水準儀,讓觀測視線垂直當地重力方向。兩尺讀數之差值,即為觀測所得之高程差。而逐站累積所得,即為所求兩點間之觀測高程差。因有儀器定平之操作程序,故其物理意義為在單站測量時,所得之視線為垂直當地重力方向。然而,各地重力值並非一致,故觀測高程差與測量之路線相關,不同之路線會產生不同之觀測高程差。單一兩站間的差值雖然小到無法以水準測量獲得,但是累積以後的量可以很可觀,因此原始逐差水準所獲得的觀測高程並不符合「物理」性質精確之要件,於測量區域增大或要求精度較高時便不適用,必須將重力也考慮而得到精確值。……【更多內容請閱讀科學月刊第575期】