- 專欄
文章專區
2017-11-01夾在中間的無限大?
575 期
Author 作者
游森棚/任教於臺灣師範大學數學系及空軍官校。
最近「集合論(Set theory)」有一個大進展,在此和讀者分享。
我就讀中班的兒子已經會從1數到100,問他6 張樸克牌1、2、3、4、5、6和3張樸克牌2、4、 6哪一個比較多,他可以毫不猶豫地說前者比較 多,6張當然比3張多啊!
但是,所有的數學系學生都要經過底下奇妙的第 一關:1、2、3、4、5、6、7、8…… 和 2、4、 6、8……哪一個比較多?兩者都是無限大沒錯,但答案是「一樣多」。但是,明明2、4、6、8…… 只有1、2、3、4、5、6、7、8……的一半不是嗎? 怎麼會一樣多呢?
所謂的一樣多是什麼意思?數學的嚴格語言讓 我們可以精確描述,沒有模糊空間, 因此需要 集合論。1、2、3、4、5、6 比 2、4、6 多,是 因為沒辦法把兩邊的東西兩兩相配對而一個不 剩,即無法在兩個集合A = {1, 2, 3, 4, 5, 6}與 B ={2, 4, 6}的元素間找到一一對應,舉例來說:
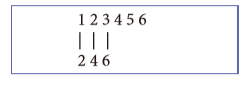
數學的說法是如果可以在兩集合A與B之中找到一個能一一對應 的函數,則 A的基數(cardinality,姑且將之想為元素個數)就和B的基數一樣大,我們姑且就稱2個集合一樣多。
所以用以下的對應法,可以證明自然數N = {1, 2, 3, 4,...}與2N = {2, 4, 6, 8,...}一樣多:
.PNG)
接著就會出現很有趣的習題,例如有理數也跟自然數一樣多,平面上所有坐標是整數的點也跟自然數一樣多。這些集合都有無限多個元素沒錯,但都可以找到方法和自然數一一對應,也就是說可以一個一個編號去數,所以這種無限大叫做「可數的無限大 (countable infinity)」,代表的集合就是正整數N。
但是,數學系的學生還要過第二關:介於0~1之中的所有實數比所有的自然數還多。數學家康托(Georg Cantor)給出非常有名、 近乎神乎其技的「對角線證明」,想法如下:
首先,0~1 之中的所有實數當然有無限多個,現在假設介於0~1 之中的所有實數和自然數一樣多(可數無限多), 那就可以全部一個一個列出來,把它們都寫成無窮小數,例如按以下的順序寫:

然後,我們設計一個新的小數α,它的小數點後第一位 與 α1 不一樣,小數點後第二位與 α2 不一樣,小數點後第 一位與α3 不一樣…以此類推。……【更多內容請閱讀科學月刊第575期】