- 專欄
文章專區
2018-07-01歐拉數與歐拉的數
583 期
Author 作者
游森棚/任教於臺灣師範大學數學系及空軍官校。
在數學多個領域留下許多重大發現的數學家歐拉,許多的數學公式、方程式或定理都因他而生,就連最簡單、直接以他之名來命名的數列,都還得細分 成Euler number 和Eulerian numbers······
歐拉(Leonhard Euler, 1707~1783) 是瑞士數學家,也是有史以來最偉大的數學家之一。數學上幾乎「每一個」領域都有以他命名的定理,而且都是開創性的結果。從平面幾何到一筆畫問題;從流體力學的歐拉方程到代數拓樸與多面體理論的歐拉示性數;從數論到分析,其深度與廣度真的讓人嘆為觀止。
在組合數學中歐拉也做了許多原創的工作。我的專長是組合學,歐拉理所當然成為我最景仰崇拜的數學家,就連最基礎的排列—— 討論把 1、2、 ……、n 排成一列的理論, 都有2個數列以他命名:一是Euler number,另一是Eulerian numbers。
《科學月刊》一直希望專有名詞要有中文翻譯,現在可能要踢到鐵板——前者是「歐拉數」,後者是「歐拉的數」。這兩個數在數學上都非常重要,雖然兩者定義超級不同,但是歐拉居然找到把兩者聯繫起來的關係。
前陣子我與幾個合作者共同發表一篇論文,推廣了歐拉的這個結果,在這裡把問題的始末跟讀者分享。
歐拉數這個專欄中曾經介紹過「歐拉數En」, 這個數是計算1、2、……、n 的排 列中,有多少個長得像是下上下上下上……的形狀。這種排列稱為交錯排列 (alternating permutations), 比如 長度為4的這種排列有5個,分別是
4132、4231、3142、3241、2143
所以E4=5。
而這個數列的前幾項是
〈En〉n≥0=〈1、1、1、2、5、16、 61、272、1385···〉
歐拉數和三角函數有奇妙的聯繫。如果 用大一微積分把tanx 用泰勒展開式展 開(亦即用多項式去逼近), 可以得到
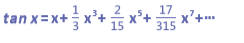 這樣看起來沒什麼,但是若把xn 的 係數調成n!,這個式子就變成
這樣看起來沒什麼,但是若把xn 的 係數調成n!,這個式子就變成
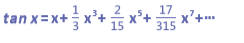 那些係數就是奇數項的歐拉數!讀者要問,那偶數項的跑哪去呢?答案是 secx的泰勒展開式
那些係數就是奇數項的歐拉數!讀者要問,那偶數項的跑哪去呢?答案是 secx的泰勒展開式
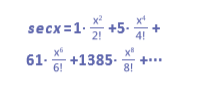 因此,tanx 和secx都有組合意義,當代組合學宗師史丹利(Richard Stanley) 幾年前寫了一篇歐拉數的總介紹,有興趣的讀者非常值得一讀。
因此,tanx 和secx都有組合意義,當代組合學宗師史丹利(Richard Stanley) 幾年前寫了一篇歐拉數的總介紹,有興趣的讀者非常值得一讀。
歐拉的數
「歐拉的數An,k」的定義則完全不同: 寫下一個排列,比如526314,我們 看看有多少個 「下降(descent)」, 在此例中是3 個,分別是52、63、 31。則歐拉的數便是在數1、2…n的 排列中,有多少個剛好有k個下降, 比如長度為3 的六個排列,123、 132、213、231、312、321,下降分別是0、1、1、1、1、2個,因此
A3,0=1 A3,1=4 A3,2=1
……【更多內容請閱讀科學月刊第583期】