文章專區

Take Home Message
• 貝茲曲線由法國工程師貝茲提出，起初應用在設計汽車的曲線上，後來也大量運用於文字設計、電腦排版、飛機與建築設計、動畫繪圖，甚至是機器人及自動駕駛領域中。
• 藉由調控貝茲曲線的控制點，可以產生一次貝茲曲線、二次貝茲曲線、三次貝茲曲線，以此類推，而一次貝茲曲線為大家熟知的直線。
• 貝茲曲線的優勢包括可預測性、穩定性、仿射不變性、平滑性與連續性，這些性質讓設計師和工程師免去手動繪製，藉由參數的改變就能精確控制形狀，創造出流暢優美的曲線。

什麼是貝茲曲線？與美學有什麼關聯？

貝茲曲線（Bézier Curve）是一種用於繪製平滑曲線的數學工具，廣泛應用於電腦圖形學、動畫設計、字體設計、電腦輔助設計（computer-aided design, CAD）、機器人學以及遊戲開發等領域。

 
寶獅（Peugeot）汽車204 是第一款使用電腦輔助設計，利用貝茲曲線設計外型的車款。（Adobe Stock）

這種曲線最早由法國工程師貝茲（Pierre Bézier）於20 世紀60 年代提出，最初運用於汽車工業的曲線設計，像是在車身的流線造型上。而貝茲曲線的優點是它可以透過少量的控制點（control points）來產生平滑可控的曲線，不需要手動繪製大量細節，這個特點讓貝茲曲線在數字設計與電腦視覺（computer vision）領域具有極高的應用價值。

貝茲曲線的數學理論

貝茲曲線是一種參數曲線，它的基本概念是使用一組 「控制點」來定義曲線的形狀（圖一）。然而這些控制點並不一定落在曲線上，而是間接影響曲線的整體形態。

在貝茲曲線中，伯恩斯坦多項式（Bernstein polynomials）是貝茲曲線公式的基礎，我們先來看看伯恩斯坦多項式的公式：
b_v,n (x) = [n,v] x^v(1-x)^n-v，for v=0,…,n,
舉例來說，當v=2, n=5 套入上方公式時，便以下方數學式表示：
b_2,5 (x) = [5,2] x²(1-x)³ = 10x²(1-x)³
而v=0, n=0,1,2,3；v=1, n=1,2,3；v=2, n=2,3；v=3, n=3 時：
b_0,0 (x) = 1,
b_0,1 (x) = 1-x  ，b_1,1 (x) = x
b_0,2 (x) = (1-x)²，b_1,2 (x) = 2x(1-x) ，b_2,2 (x) = x²
b_0,3 (x) = (1-x)³，b_1,3 (x) = 3x(1-x)²，b_2,3 (x) = 3x²(1-x)，b_3,3 (x) = x³
從上方例子可以看出伯恩斯坦多項式具有對稱性及遞迴性，另外它還有一特點，那就是歸一性，如下方公式，總和加起來會等於1 的特性：

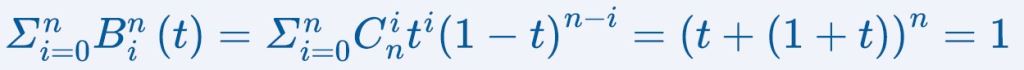
也因為這些特質構成了貝茲曲線的對稱性與美感。另外，伯恩斯坦多項式也是在數值分析及逼近論中相當重要的函數喔！

一次貝茲曲線

一次貝茲曲線也被稱為線性貝茲曲線，線性是最簡單的形式，也就是一條直線，由兩個控制點P0 和 P1 所定義，……【更多內容請閱讀科學月刊第664期】