- 專欄
文章專區
2025-01-07從數學、建築到政治 全才的美國總統傑佛遜
661 期
Author 作者
劉柏宏 | 勤益科技大學基礎通識教育中心教授
Take Home Message
• 起草《美國獨立宣言》的總統傑佛遜不僅是一位多才多藝的政治家,還熱愛數學,可說是美國歷史上極具創意和智慧的領袖之一。
• 傑佛遜曾提出「傑佛遜法」來分配國會眾議員席位。他引入最大平均除數的概念,以數學化方法確保各州國會席位分配的相對公平性。
• 傑佛遜在1819 年創立維吉尼亞大學並親自設計校園建築,將數學、美學和建築完美融合,體現了他對比例、和諧與美的深刻理解。
去(2024)年美國總統和國會選舉結束,常被評為失態的川普(Donald Trump)當選了第60 任美國總統,即將於今(2025)年1 月20 日就職。美國經常自我標榜為全世界民主國家的楷模,但川普在第一任總統任期內引起的紛爭,卻曾引來諸多對美國民主的嘲諷。尤其是對比本文即將要介紹的第三任總統,同時也是《美國獨立宣言》(The unanimous Declaration of the thirteen united States of America)主要起草人――傑佛遜(Thomas Jefferson,圖一),不免讓人覺得美國「政風日下」。
.jpg)
圖一 | 美國第三任總統傑佛遜
(Rembrandt Peale, public domain, Wikimedia Commons)
傑佛遜不僅在政治上表現出色,他在各領域的全才表現更被譽為是一位足以和達文西(Leonardo da Vinci)比擬的「文藝復興人」(Renaissance man)。此外,他對於數學的熱愛在歷屆美國總統中可能無人出其右,之所以說「可能」是因為美國第20 任總統加菲爾(James Garfield)於1876 年擔任國會議員期間,曾發表一個關於畢氏定理的證明。傑佛遜雖然未曾發表過任何數學上的發現,但他對於數學的熱愛與實踐令人稱佩,所以一些數學史家和科學史家都曾撰文述說他的貢獻。
傑佛遜在進入美國威廉與瑪莉學院(William and Mary College) 前寫給他的監護人哈維(John Harvie)的信中就提到,上大學的好處之一就是「學到一些數學」。他從歐幾里得(Euclid)的《幾何原本》(Elements)書中,見識到數學的邏輯演繹嚴謹之美;從牛頓(Isaac Newton)的《流數法》(Method of Fluxions)、《自然哲學的數學原理》(Philosophiæ Naturalis Principia Mathematica)和《光學》(Opticks)等著作中,領略了數學在物理世界的實用之真。大學期間,傑佛遜受教於數學家史莫(William Small),也因此更熟悉洛克(John Loche)、培根(Francis Bacon)、牛頓等三位英國經驗主義者的著作。
傑佛遜在1785 ~ 1789 年間擔任法國大使,此時適逢法國的數學領域發展逐步邁向顛峰,他也因此認識不少數學家。例如他就稱讚拉格朗日(Joseph Lagrange)是當世最偉大的數學家。此外,他更見識到跟隨萊布尼茲學派的歐陸數學已超越堅守牛頓風格的英國數學,於是積極呼籲美洲新大陸的數學家要改向歐陸數學學習。
數學計算與政治算計
美國國會分為參議院和眾議院,各州在參議院中均有兩位議員代表(與各州人口無關),眾議員人數則取決於該州的人口數。1791 年美國國會立法通過眾議員有120 人,每州至少應有眾議員一人,其餘名額就按照聯邦所轄各州的人口數目依比例分配,例如每三萬人口可以分配一位眾議員。然而依此計算出的比值並非都是整數,但各州眾議員名額都是整數,小數部分該如何處理?
做法可以有很多種,例如四捨五入法。但如此一來比值為1.51 的州有兩席,1.49 的州只分到一席,實屬不公。或是也可以先將比值小數點部分都略而不計,先依據整數位分配給各州席位。這樣計算後所剩下的席位又會有兩種分法:第一,把剩下的席位依序分配給人口較多的州;第二,根據小數部位大小依序分配給小數部分較大的州。不過前者被批評為獨厚人口較多的州,後者則與州的人口大小無關,而是依損失的比例大小依序補償,看來較為公平。因此美國國會通過第二種算法,並命名為「漢密爾頓法」(Hamilton Method)〔註〕。
〔註〕此計算方式由時任財政部長的漢密爾頓(Alexander Hamilton)所提出。
* V:維吉尼亞州、N:紐約州、M:麻薩諸塞州、C:康乃狄克州、D:達拉威爾州
但是時任國務卿的傑佛遜獨排眾議,他反倒認為漢密爾頓法違反憲法主張眾議員必須按照聯邦所轄各州的人口數目,並依比例分配的原則。依據當時憲法的規定,每三萬人可分配一名眾議員,假設某州比值的小數位為0.9,是所有州的比值中最大的小數位,依據漢密爾頓法該州應增加一席,這表示該州直接以2.7 萬人取得一席,違反憲法規定。時任美國總統的華盛頓(George Washington)贊成傑佛遜的論述,因而動用第一次否決權否決漢密爾頓法,取而代之的是「傑佛遜法」(Jefferson Method)。
傑佛遜法建立於存在一個「最大平均除數」的原則之下。傑佛遜認為既然要依照比例,那麼在公平原則之下,只能有一個共同的除數去計算席次。為清楚介紹如何尋找這共同的除數,並交代其中隱含的脈絡,本文參考科學史家科恩(Bernard Cohen)書中的假想數據說明:
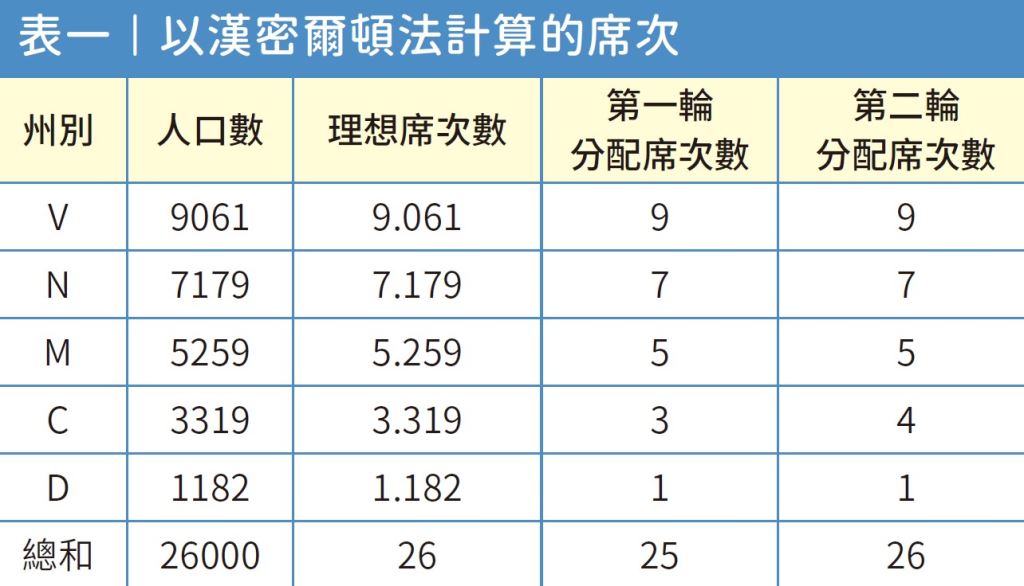
假設紐約州(State of New York)、維吉尼亞州(Commonwealth of Virginia)、麻薩諸塞州(Commonwealth of Massachusetts)、康乃狄克州(State of Connecticut)、達拉威爾州(State of Delaware)五個州的人口總數為2 萬6000 人(表一)。若每1000 位產生一位眾議員,總共可以產生26 席眾議員。從表一中可以看出第一輪忽略小數部位後這五個州分別分配到9、7、5、3、1 個席次,還空餘一席。而康乃狄克州的小數位最大,為0.319,依據漢密爾頓法可以獲得此一席。
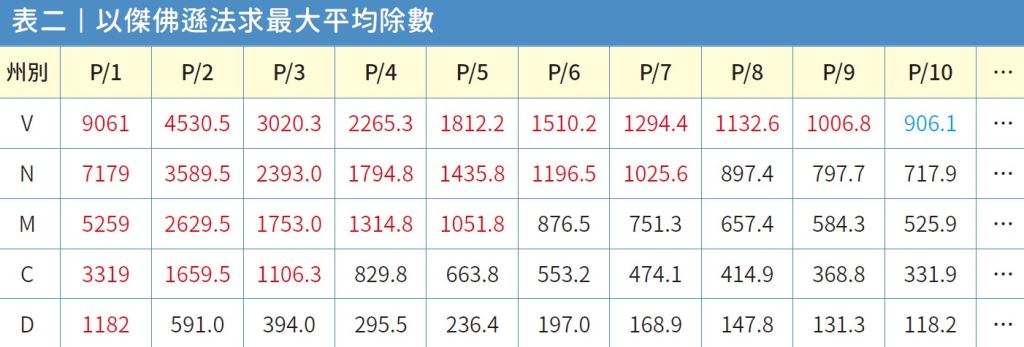
此案例若採用傑佛遜法計算,首先將各州人數P 分別除以1、2、3、4…,直到產生最大平均除數就停止。但該如何確定最大平均除數呢?就是從所有平均數依據大小排列出位居第26 順位的平均數,計算後可以找到此案例中的最大平均除數就是維吉尼亞州的人數除以10(P/10),可以得到藍色的數字906.1,其餘共有25 個紅色數字大於906.1。再用「最大平均除數」也就是906.1 去除各州人口數,最後取整數部位即為各州席次數。由於傑佛遜法沒有小數進位問題,也就可以避免掉漢密爾敦法因小數進位所產生違憲的狀況。
* V:維吉尼亞州、N:紐約州、M:麻薩諸塞州、C:康乃狄克州、D:達拉威爾州
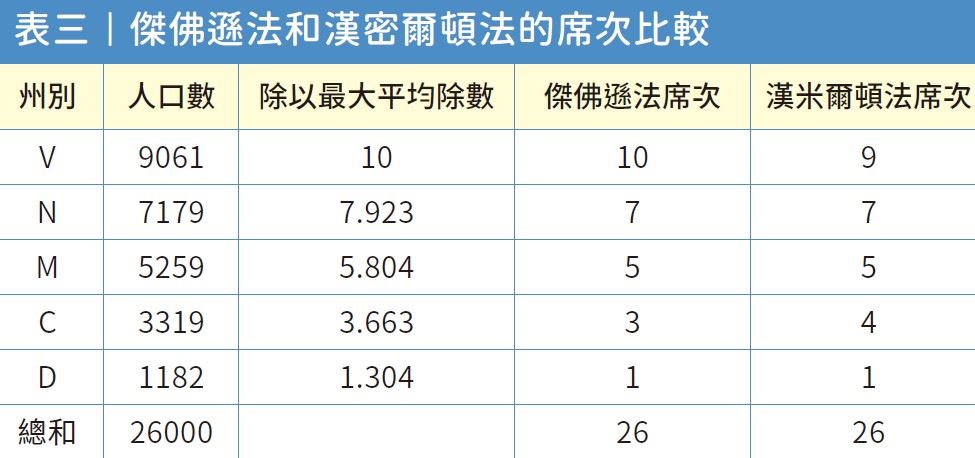
比較用傑佛遜法和漢密爾頓法計算後的眾議員席次,可以發現兩者只有一席之差,「傑佛遜法」有利於維吉尼亞州,「漢密爾頓法」有利於康乃狄克州。
* V:維吉尼亞州、N:紐約州、M:麻薩諸塞州、C:康乃狄克州、D:達拉威爾州
既然差距如此微小,何必如此大費周章地計算?且維吉尼亞州僅比9000 人多61 人就多獲得一席,而康乃狄克州多出的319 人卻被歸零,如此看來真的公平嗎?其實政治不全然是數學,由於當時美國南方州和北方州因為解放奴隸問題立場不同而仍有嫌隙,康乃狄克是北方州、維吉尼亞則是南方州,且華盛頓和傑佛遜都出身維吉尼亞州,所以也有人提出異議,認為這是以「數學計算」進行的「政治算計」。……【更多內容請閱讀科學月刊第661期】