文章專區

Take Home Message
• 量子化學的發展從薛丁格方程式到價鍵理論和分子軌域理論，目前已可利用量子力學計算預測分子結構。
• 化學鍵形成的過程中，動能和位能的變化扮演關鍵角色。不同化學家也對化學鍵的結合能提出不同觀點。
• 罕德悖論提出了分子結構與量子力學的矛盾之處，化學分子的本質可能比我們想像的更加複雜和難以捉摸。

1926 年初，薛丁格（Erwin Schrödinger）以德布羅意（Louis de Broglie）的物質波假設為基礎，提出了描述量子力學波行為的方程式。這個數學模型稱為薛丁格方程式，更在後來成為量子力學的核心，定義量子系統允許的穩態（stationary state），並描述了物理系統的量子態如何隨時間變化。物質由稱為「波函數」的數學函數描述，波函數提供了「預測測量結果機率」的手段。以薛丁格方程式為基礎，薛丁格能在質子產生的電位阱中檢視電子來計算氫的能階，而該計算準確地再現了波耳模型的氫原子能階。

量子化學的發展歷程

海特勒（Walter Heitler）和倫敦（Fritz London）在1927 年發表的一篇文章通常被認為是量子化學史上的第一個里程碑。這篇文章將量子力學首次應用於雙原子氫分子，進而用於解釋化學鍵。鮑林（Linus Pauling）則在1930 年代撰寫了一系列文章，將海特勒、倫敦、杉浦義勝、王守競關於價鍵理論（Valence Bond Theory，簡稱VB 理論）概念和量子力學基礎的工作整合到一個新理論框架中。鮑林在1939年的著作《化學鍵的本質》（The Nature of the Chemical Bond）中總結了VB 理論， 並以化學家可以理解的方式解釋了分子量子力學，此書將許多化學家引入了量子化學領域。

在VB 理論建立後的幾年，透過罕德（Friedrich Hund）、密立根（Robert Mulliken）、斯萊特（John Slater）等人的努力，發展出了分子軌域理論（Molecular Orbital Theory，簡稱MO 理論）。1933 年，MO 理論被公認為有效且有用的理論，透過波函數疊加原理和包立不相容原理，VB 理論可以被置於更廣泛的分子軌域（molecular orbital, MO）量子力學背景中。這兩個原理不但更精確地奠定原子軌域組成分子軌域的類型，並且解釋兩個電子自旋配對的必要性。本文因篇幅有限，不介紹詳細的技術細節，但其中最主要的結果是氫分子的波函數可以將兩個氫原子的軌域以兩種不同方式疊合――（1）兩個原子軌域波函數相加，產生建設性干涉，形成𨫡結分子軌域（bonding MO）；或（2）兩者相減產生破壞性干涉，形成反𨫡結分子軌域（antibonding MO）。

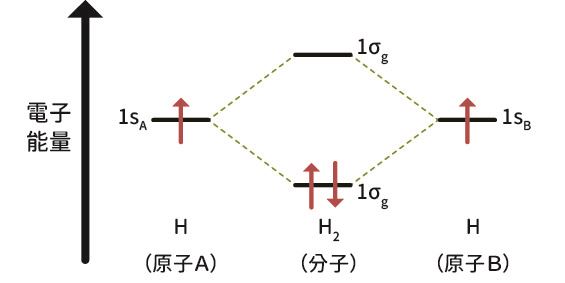
透過分子軌域模型描述兩個氫原子如何形成氫分子的鍵結，氫原子A 與B 各自的1s 軌域，可以組合變成能量較低的鍵結軌域，以及能量較高的反鍵結軌域，當兩個氫原子的電子都填在能量較低的鍵結軌域，此時兩顆氫原子就會形成能量更低的氫分子。
（資料來源：作者提供）

化學鍵如何形成？

VB 理論與MO 理論發展數十年之後，由於科學計算的興起，考量到程式設計便利性與演算法效率，後來的量子化學計算發展大多以MO 理論為基礎，逐漸走上更複雜且更精細的計算。直到今天，量子化學計算可以達到所謂化學準確度（chemical accuracy），也就是約4000 焦／莫耳（J/mol）。只不過，能夠計算化學分子並不等於能夠了解化學分子，這是本文希望討論的故事。

理論上，我們解出薛丁格方程式，就可以得到分子的所有資訊。或者，正如狄拉克（Paul Dirac）的名言：「大部分物理學和整個化學的數學理論所必需的基本物理定律是完全已知的，困難在於，精準套用這些定律會導出過於複雜難解的方程式。」但是，化學真的那麼簡單嗎？如果我們關注分子及分子中化學鍵的概念，確實可以透過求解適當的方程式來獲得它們的所有數值性質，例如鍵能與鍵長；而透過哈密頓算子（Hamiltonian）則能夠獲得能量和波函數，進一步計算其他物理量。但這仍然沒有回答到化學最基本的概念性問題――化學鍵到底是什麼？

1916 年，路易士（Gilbert Lewis） 在論文中提出了第一個價電子模型。他將化學鍵對應成共享的電子對，並用符號「：」將H₂ 分子與其中的鍵結表示為「H : H」。冒號中的兩個點「：」代表共用的電子對，以形成二個氫原子之間的共價𨫡。這個模型可以解釋有機化學中大部分的共價𨫡（例如碳為什麼形成四個立體的𨫡）。但路易士模型同時也暗示了放在兩個質子之間的兩個電子所給予的正負電荷吸引力位能，是將兩個氫原子綁在一起、形成分子的原因。真的是這樣嗎？讓我們來看看量子力學怎麼說。

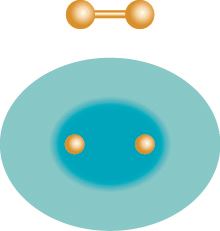
二氫陽離子的（上）球棍模型（ball-stick model）與（下）電子軌域分布模型。
（資料來源：作者提供）

為了簡化問題，我們可以從少一個電子的二氫陽離子（H2+）來討論。這個化學系統由兩個氫原子核（質子）組成，它們共享一個電子，也是最簡單的分子離子，因此在理論和實驗物理中是重要的研究對象。在此系統中，電子的總能量H ＝ T ＋V，可以清楚地分成動能T 和位能V 。當一個質子和一個氫原子互相接近時，到底是電子的動能降低還是位能下降促成分子形成？理論化學家在這個問題上一直有兩派不同的看法。赫爾曼（Hans Hellmann）及魯登伯格（Klaus Ruedenberg）提議「減少電子運動的動能」是共價鍵的關鍵黏合原因；考慮德布羅意波長λ ＝ h/p ，當一個質子和一個氫原子互相接近時，電子的非局域化會使波長變長、動量變小，而它對應的動能會因此下降。另一派看法則認為，化學鍵結合能的吸引力主要部分是由（靜電）位能的能量下降，而動能對此的貢獻會造成排斥。這種靜電位能的觀點最初是由斯萊特（John Slater） 於1933 年提出，1939 年得到費曼（Richard Feynman）的支持。後來庫爾森（Charles Coulson）也支持靜電位能的觀點，他在1952 年撰寫的著作《原子價》（Valence）對化學界產生了重大影響。

透過量子化學的計算，我們能夠分別得到動能與位能對於鍵結的貢獻。下圖描述了二氫陽離子在鍵結形成的過程中，動能部分與位能部分的變化。當質子由遠方靠近一個氫分子時，系統的動能會下降，……【更多內容請閱讀科學月刊第661期】

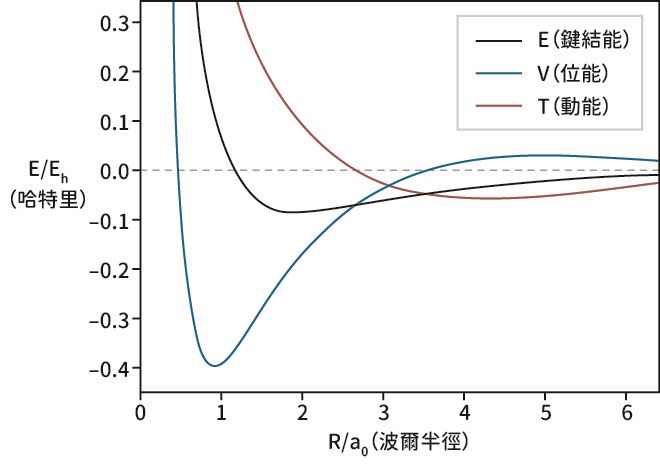
二氫陽離子的鍵結能總能（黑線）、其中的位能（藍線）與動能（紅線）的貢獻。橫軸單位為波爾半徑（0.529 Å），縱軸單位為哈特里（Hartree，1 Hartree ～ 27.21 eV），為兩倍氫原子的游離能。
（資料來源：修改自Molecules, 2020）