- 專欄
文章專區
2024-11-11從柏拉圖立體到球形多面體 艾雪的球面鑲嵌
659 期
Author 作者
林家妤 Sharkie Lin | 喜歡新奇有趣的事物,像 是數學藝術創作、策展、 採訪、寫作、創意教學、 博物館規劃。
Take Home Message
• 在艾雪博物館出的球形立體作品中,艾雪將12 隻蜥蜴形狀無縫交錯排列在球面上,展現出獨特的鑲嵌藝術。
• 球面鑲嵌需要考慮高斯曲率,然而平面圖形無法直接套用到球面,所以必須使用變形的球面多邊形來設計。
• 柏拉圖多面體可作為球面鑲嵌的基礎架構,並透過外接球體方式創造出精確的球面幾何圖案。
幾年前,筆者拜訪荷蘭鹿特丹的艾雪(Maurits Cornelis Escher)博物館時,癡迷地在博物館中逛了五個多小時。走到博物館商店時,更是被一件立體作品深深吸引。那是一顆手工感強烈、充滿幾何圖案的球(圖一),球上的圖案十分令人驚豔,它是艾雪著名的鑲嵌藝術――12 隻形狀相同的蜥蜴彼此連接又無縫交錯,將圖案從熟悉的平面躍升為立體的作品。

圖一|艾雪球(作者提供)
這樣的圖案不僅僅是視覺上的藝術創作,背後其實還隱藏著深刻的數學結構。正是數學的力量,使得這些看似無限延展的圖案能夠在球面上完美呈現。接下來,我們將從多面體開始,探索如何透過幾何學來解釋這種結合數學與藝術的獨特設計。
柏拉圖多面體
球面鑲嵌(spherical tessellation 或spherical tiling)指的是將幾何圖形無縫地排列在球面上。這種圖案的構造會將球面分割為許多等面積的小區域,這些區域可以是球面三角形、正方形、五邊形等。若想理解和製造出這樣的鑲嵌圖案,就需要運用球面幾何學(spherical geometry)的知識。
在討論球面幾何學之前,讓我們先從三維空間的正多面體談起。在三維空間中有五種正多面體,分別為正四、六、八、十二、二十面體,也被稱為柏拉圖立體(Platonic solid,圖二)。柏拉圖立體是鑲嵌幾何學的一個重要基礎,特別是當我們從平面鑲嵌過渡到三維空間時,這些立體可以為球面鑲嵌提供結構上的支撐。
圖二|柏拉圖立體
(Image by pikisuperstar on Freepik)
高斯曲率與球面幾何
然而,由於球面本身是一種曲面,當我們想要從平面轉向球面的時候,無法直接將平面上的多邊形套用於球面上,因為平面與球面的高斯曲率(Gaussian Curvature, K)〔註〕並不相同。
〔註〕高斯曲率能用於描述表面的彎曲程度,是主曲率K1 與K2 的乘積。
平面的曲率為0,而球面為正曲率,雙曲面則為負曲率。這種曲率的差異使得我們無法像在平面上那樣簡單地排列正多邊形,還必須考量變形的特性(圖三)。例如在球面上的三角形會稍微變形,內角和也會大於180°。
.jpg)
圖三|高斯曲率與三角形
(游佳宜繪製;Keng, https://reurl.cc/kygRz3)
也就是說,,為了在球面上進行鑲嵌,我們需要考慮如何將平面多邊形變形,使這些多邊形適應球面的彎曲。因此只能使用變形的球面多邊形(spherical polyhedron),例如球面三角形、球面正方形或球面五邊形等進行鑲嵌,這些形狀的邊也不再是直線,而是球面上的「弧線」。
球面幾何學
接著,我們可以利用先前提過的柏拉圖立體作為構建球面鑲嵌的架構。具體方法是以正多面體外接球體(circumscribed sphere)的方式,定義出球面上的頂點,再繪製兩點之間最短路徑的大圓弧,並將正多面體的邊描繪出來就可以得到球形正多面體(圖四)。例如正二十面體由20 個正三角形組成,這些三角形能作為球面鑲嵌的基本單元,只要在上面設計有趣的圖案,就可以達到球面鑲嵌的效果。
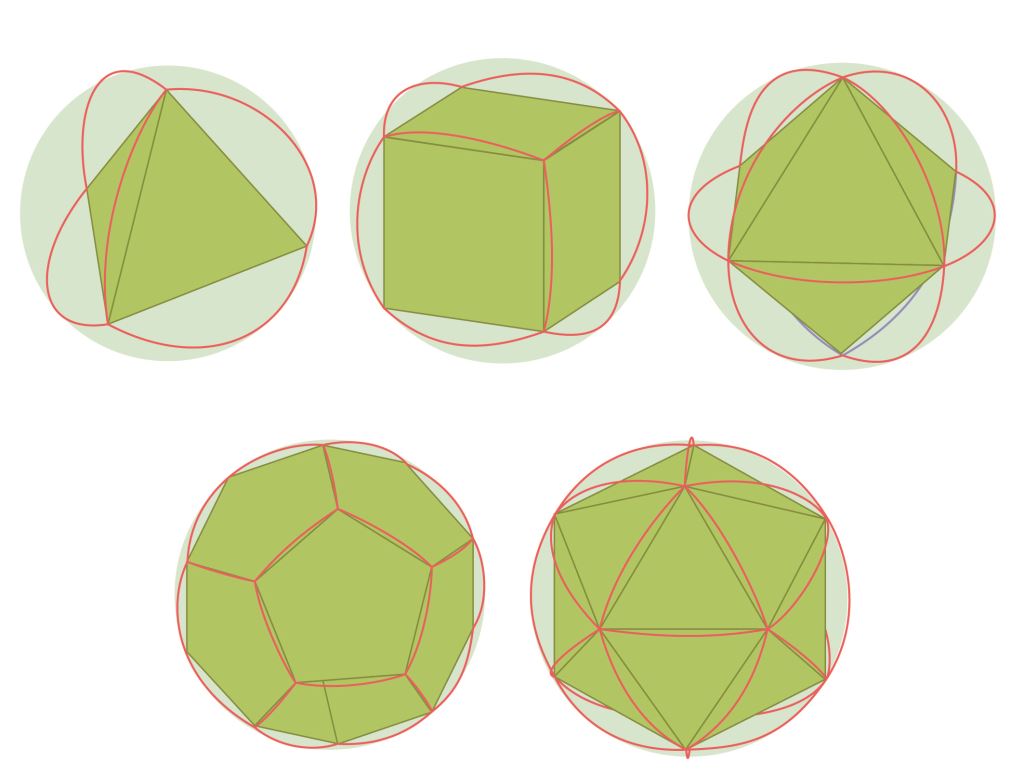
圖四|五種正多面體與填滿球面的球面多邊形
(游佳宜繪製;Lei & Qi. 2020.)
不過要使用單一形狀無縫地填滿球面,不只有正多面體能達成,各種不同的球面三角形也能夠填滿球面。例如筆者自己的數學藝術創作「吠陀球」(Vedic sphere,圖五),讀者可以看到圖五的球體被六個圓分割,球面上排列著90°- 60°- 60°的球面三角形,彼此無縫相連,將整個球面畫分為24 個區域。

圖五|筆者的數學藝術創作「吠陀球」,獲選Bridges 2020 芬蘭全球數學藝術展作品。(作者提供)
在筆者的吠陀宇宙系列創作中,吠陀球是基於吠陀立方的對稱面進行球型化的作品。原本吠陀立方的六個對稱面(X = Y, Y = Z, X = Z, X + Y = 9,Y + Z = 9, X + Z = 9)從矩形轉化為圓形,吠陀球的製作選擇了內切球(inscribed sphere)的方式,主要是考量對稱面本身加工製作的便利性,與上述多面體的外接球變形有些不同。
然而,當我們探討球面多面體時,通常會選擇外接球的方式來進行轉化,因為這樣可以讓多面體頂點與球面相接觸,確定每個頂點的位置。無論是強調每個面與球面接觸的內切球,或者是確保頂點幾何對應的外接球,這兩種方法都能實現球面鑲嵌,並應用於不同的幾何創作,展現美妙的球面圖形。
球面幾何學相較於平面而言更加複雜且精密,這是因為球面具有曲率,且沒有明確的起點與終點。這種無限延伸的特性使得球面成為探索幾何圖案及藝術表現的絕佳載體。正因如此,球面可以更好地呈現艾雪作品中的「無限」概念。
艾雪的鑲嵌圖案展現了藝術與數學的完美結合。將這些平面設計轉化為球面上的鑲嵌,需要更深入的數學技巧與對曲面的精準掌握,正是透過這些知識與技巧,才能讓艾雪的設計在三維空間中得以實現,呈現出無限的視覺魅力。

吠陀球的幾何模型,同時也是四角化立方體的球型化(Tetrakis hexahedron,又稱四角化六面體、四六面體)。四角化立方體是一種卡塔蘭立體(Catalan solid),可以當作是在立方體的每個面上放上正四角錐的結果,所以才會以四角化描述此種特性,外觀上看起來有24 個全等的等腰三角形。(Watchduck, CC BY-SA 4.0, Wikimedia Commons)
延伸閱讀
1. M.C. Escher Collection, https://mcescher.com/
2. 俞韋亘(2024)。歐拉示性數 每一面都是六邊形的球體有可能存在嗎?。科學月刊,653,44–47。
3. Purss, M. B., et al. (2019). Datacubes: A discrete global grid systems perspective. Cartographica: The International Journal for Geographic Information and Geovisualization, 54(1), 63–71.