- 專欄
文章專區
2024-10-14何設計太空軌道? 探索宇宙的成敗關鍵
658 期
Author 作者
蕭富元 淡江大學航空太空工程學系教授
Take Home Message
• 軌道力學發展於17 世紀克卜勒和牛頓的理論,為太空探索奠定基礎。1957年蘇聯首次將人造物體送入地球軌道,開啟太空探索時代。
• 太空軌道設計涉及複雜的物理和數學計算,不同任務會依目的選擇不同類型的軌道,例如地球同步軌道、拉格朗日點、低能量轉移軌道等。
• 軌道設計失誤會導致嚴重的後果,隨商業太空活動興起,軌道設計將面臨碰撞風險管理、軌道碎片清理、法規制定等多重挑戰。
在探索太空的歷史中,軌道設計的科學一直是不可或缺的一部分。從最早的人造衛星到現代的深空(deep space)探測任務,軌道設計讓我們能夠精確地將太空船或探測器送達指定位置,進行科學實驗,甚至是日後的外太空殖民。
軌道力學的起源
現代軌道力學的起源,可追溯至德國天文學家克卜勒(Johannes Kepler)在17 世紀初提出的行星運動三大定律。這些定律是他對丹麥天文學家第谷(Tycho Brahe)觀測數據的分,描述了行星如何圍繞太陽運行。之後英國科學家牛頓(Isaac Newton)在1687 年出版《自然哲學的數學原理》(Philosophiæ Naturalis Principia Mathematica)提出萬有引力定律,和他更早之前提出的運動定律共同解釋行星、衛星、其他天體的運動行為,奠定了軌道力學的基礎,並成功解釋克卜勒行星運動定律。
牛頓曾經提出一個著名的「思考實驗」――牛頓砲彈拋射(Newton's Cannonball),可以協助我們理解軌道力學的原理。當重力作用在拋射物上時,它會根據初速度的不同而沿著不同路徑運行(圖一):
1. 如果速度較低,拋射物將會直接落回地球。
2. 如果速度再高一點,拋射物落地點就會更遠。
3. 如果速度達到該高度的軌道速度,拋射物將會沿著固定的圓形軌道繞地球運行,並返回到它被拋射出的山峰。
4. 如果速度高於軌道速度,但不足以完全離開地球(低於逃逸速度),它將會沿著橢圓軌道繼續繞地球運行。
5. 如果速度非常高,拋射物將會以拋物線軌道(恰好為逃逸速度)或雙曲線軌道離開地球。
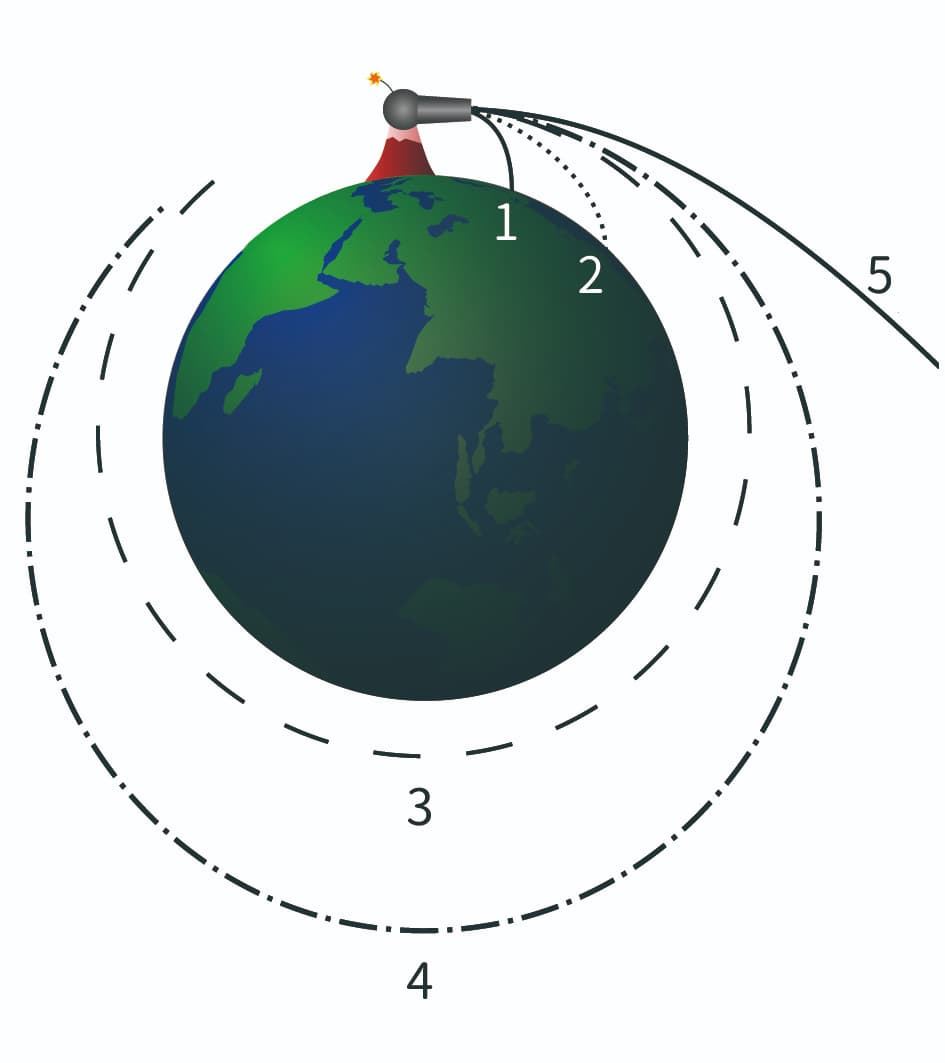
圖一 | 牛頓的砲彈拋射思考實驗
(Brian Brondel, CC BY-SA 3.0, Wikimedia Commons)
人類設計的第一條太空軌道-史波尼克1 號

史波尼克 1 號
NASA, NSSDCA/COSPAR ID: 1957-001B)
太空軌道設計的故事始於20 世紀中葉,當時國際間的太空競賽推動了衛星技術的迅速發展。在1950 年代,冷戰時期的美國和蘇聯在科技、軍事及意識形態上激烈地競爭。
1957 年10 月4 日,蘇聯寫下人類歷史上的一個重要時刻:世界第一顆人造衛星――史波尼克1號(Sputnik 1)成功發射進入地球軌道。這不僅是冷戰時期太空競賽的一個重要節點,更是人類太空史上的一次巨大突破。當時全球的觀眾還能在無線電接收器中,聽到史波尼克1 號發出的簡單「嗶嗶」聲,這聲音也成為了太空探索時代到來的宣告。
史波尼克1 號的成功發射克服了多項前所未有的技術挑戰,包括如何將一個83 公斤的金屬球體送入高達約250 公里的地球低軌道(low earth orbit, LEO),以及如何確保衛星在太空中的穩定運作。要將衛星送入地球軌道,需要極大的初速和精確的發射角度。為此,蘇聯的工程師和科學家開發R-7型運載火箭,這款多級火箭能提供足夠的推進力將史波尼克1 號送入預定軌道。R-7 火箭的成功設計後來也成為了蘇聯及俄羅斯太空探索的基石。
太空成為兩國競爭的新前線,史波尼克1 號的發射不僅展示了蘇聯的科技實力,更對美國造成了巨大的心理衝擊,促使美國政府加快了自己的太空計畫,最終成就了1960 年代的阿波羅計劃(Project Apollo)。
了解天體運動的基石-太空軌道
在太空探索的領域中,了解並利用太空軌道是實現有效太空任務的關鍵。從史波尼克1 號到現代的國際太空站(International Space Station),甚至是更遠的外太空探索任務,每一項太空探索活動都依賴著對軌道力學的精確計算和應用。
軌道設計涉及對天體物理學的深入理解,包括萬有引力定律及萬有引力對移動物體的影響。科學家和工程師必須計算太空船與中心星體,例如地球、太陽或月球之間的精確距離、速度、推進力,以確保太空船能夠進入並維持在軌道上。這些計算涉及複雜的物理和數學,必須精確執行以避免任何潛在的失敗可能。
太空軌道是物體在太空中遵循重力與其他外力,例如推力、空氣阻力等,綜合作用下的路徑。這些軌道路徑可以是圓形、橢圓形,甚至是更加複雜的幾何形狀。無論是衛星或太空船要進入並維持在特定軌道上,都必須滿足特定的速度和方向要求,這些要求由牛頓的運動定律和萬有引力定律決定。
在軌道計算中,最初步的設定就是「二體問題」(two-body problem)。二體問題有兩道假設:一、這個世界只存在兩個物體,其他物體的存在可忽略不計;二、這兩個物體都是質點。在這個設定底下,兩個物體的相對運動軌跡為固定平面的圓錐曲線,也就是圓、橢圓、拋物線或雙曲線(圖三)。另外,數學上可以證明質量均勻分布的完美球體,它的重力場與質點相同。
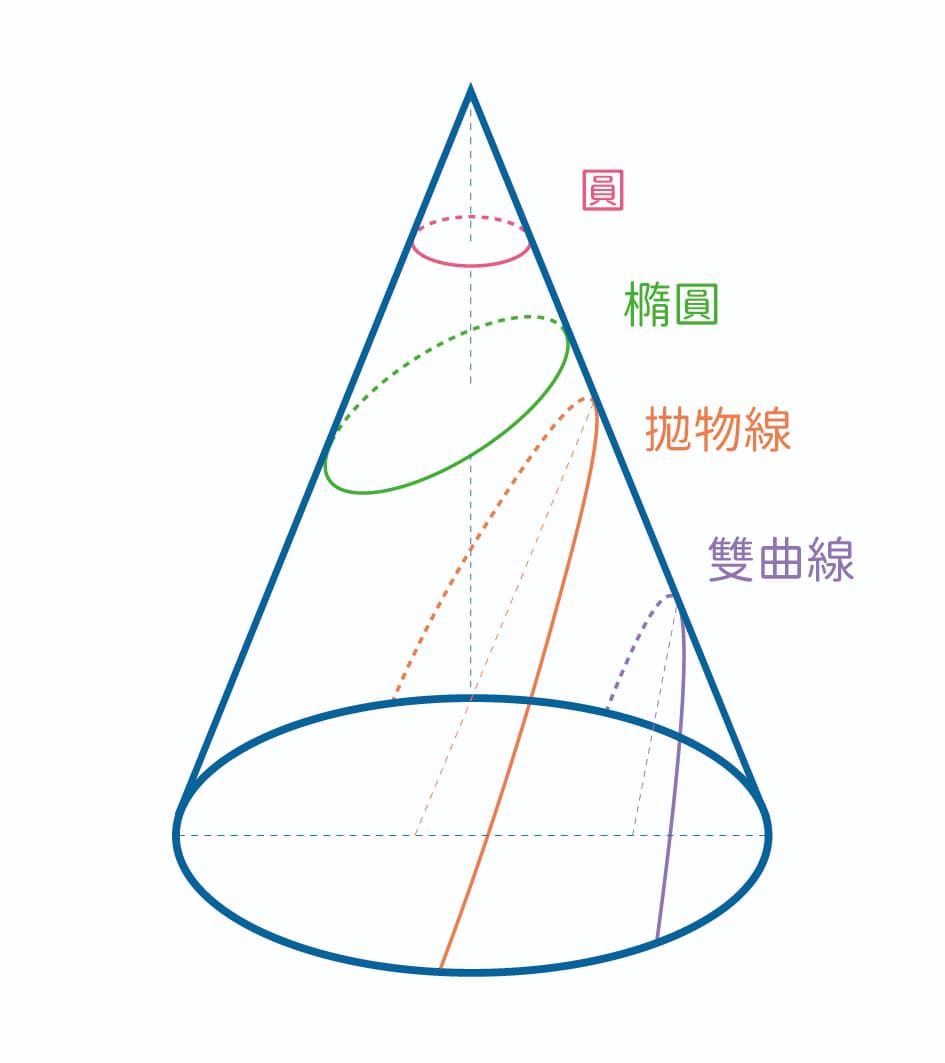
圖三 圓錐曲線圖
(Adobe Stock)
以地、日、月系統而言,約400 公里高的低軌衛星會受到這三個星體的引力比例影響,依序大約是 1 : 6.8×10⁻⁴ : 3.8×10⁻⁶。因此,在初步的軌道設計階段,忽略日、月,甚至其他星體的引力,並不會對軌道設計造成太大的誤差。然而,地球實際上並非質量均勻分布的完美球體,而是一顆矮胖型的星球。由於地球的赤道半徑比南北極半徑略長,因此繞地衛星的軌道面並非固定不變,而是繞著北極軸與軌道面的法向量旋轉。此效應又稱J2 效應。若是考量到更深入的應用,例如探月任務、定軌(orbit determination)、小行星(asteroid)探測、行星際旅行(interplanetary travel)等,則需要考慮比J2 效應更詳細的重力場模型,並納入太陽或其他星體的影響,而變成「三體問題」(three-body problem)或是「多體問題」(n-body problem),涉及到更高深的軌道力學。
太空軌道的設計邏輯如何選擇最佳軌道?
在實際應用中,不同的太空任務會依據特定用途和優點選擇不同類型的軌道:
……【更多內容請閱讀科學月刊第658期】