- 專欄
文章專區
2024-09-09《九章算數 》缺少的臨門一「角」 角 度、弦表與 三角函數的發展
657 期
Author 作者
單維彰/中央大學數學系、師資培育中心、文學院學士班合聘教授。
Take Home Message
• 古中國數學典籍《九章算術》遺留了「弧弦互算」問題,因缺乏「角」的概念而無法解決,顯現出中西方數學發展的關鍵差異。
• 角度概念在天文曆法中至關重要,中國數學因無法「弧弦互算」導致曆算落後,進而影響天文學發展。
• 托勒密製作的「弦表」可解決弧弦互算問題,它不僅是早期函數觀念的體現,也為三角函數的發展奠定了基礎。
在《科學月刊》今(2024)年3 月號刊出的〈超過300年的「倍立方」探究之旅 古希臘人對平方軌跡的探索〉一文中,作者提到古希臘數學「並無不重實用」。這邊要提供讀者另一個古希臘數學實用的例子――托勒密(Claudius Ptolemy)的弦表。弦表不但是最早的函數觀念之一,也具體呈現了三角函數(sin、cos 等)的真諦,它還是對數(log)被發明的契機。在本篇文章中,筆者想藉此談一談歷史對數學教育的啟發,特別是闡明「角」與「三角」真正應該學習的素養。
中國最偉大的數學典籍-《九章》

(中國書店海王邨公司,public domain,Wikimedia Commons)
故事要從古中國最偉大的數學典籍――《九章算術》(簡稱《九章》)說起。在進入現代之前,2000 年以來的華人數學家(以前稱為「疇人」)皆是以此書作為標準的數學入門教材。很多人寫過《九章》「有」什麼,但這裡要說它「沒有」什麼。《九章》有兩個主要的「懸念」:兩道沒有正確公式的題目。
《九章》的第一個懸念是「球體積公式」,這條公式可以作為當代文明進展的一個里程碑。這個懸念還好,不久之後就被南北朝劉宋時期的數學家祖沖之與祖暅解決了。所謂的「祖暅原理」就是在球體積公式的推論過程中出現,可惜目前的教科書都沒有善用這則美妙的歷史故事。漢文明比希臘文明晚了700 多年抵達「球體積」的里程碑,但相較於其他文明還是算早。
《九章》的第二個懸念「弧弦互算」可就嚴重了,問題發生在〈方田〉章中的「弧田」節,沒能提供一般性的「弦矢求弧」算法。在圓上任取兩點A、B,這兩點決定的線段稱為AB弦;在兩點之間且長度不超過半圓的那一段圓周,則稱為AB弧(圖一)〔註〕。在此配置中,AB弦和AB弧稱為彼此相對的弦或弧。
[註]
本文所說的「弧」都是「圓弧」的簡稱。
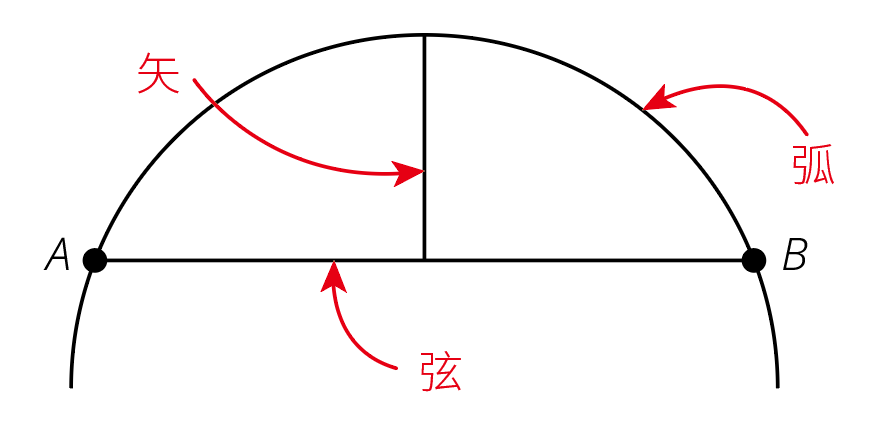
圖一|弦、弧與矢
(作者提供)
彼此相對的弦與弧圍成的平面區域,在《九章》中稱為弧田,現在則稱為弓形;在弓形內部,弦的中垂線段稱為矢。而「弦矢求弧」的題目意思是:已知弦長與矢長,如何求弧田面積?《九章》沒能給出這題的公式。而這個弧田未解的懸念,便成為中國數學的千年懸案,一直到歐洲數學傳入中國為止,華人始終沒有自己解決這個問題。
解不開的弧弦互算問題
讀者或許會說,弓形面積不就是扇形減去三角形嗎?這個觀念確實正確。三角形的其中一個頂點是圓心,假設已知的弦長為2a、矢長為b,則三角形面積為a(r-b),但扇形面積為何?古人已經
知道,假如弧長是2s,則這一段弧在整個圓中占的比例為s⁄πr,所以扇形面積是πr²× s ⁄ πr = rs 。於是可以得到「弦矢求弧」的公式(圖二):
弧田面積= rs - ar + ab
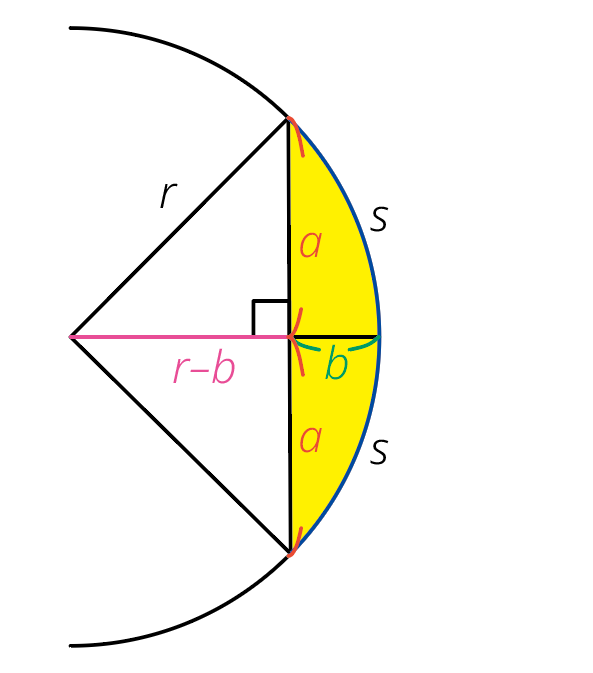
圖二|弧田面積的算法
(作者提供)
其中,圓半徑r 可以運用畢氏定理從弦矢算出來:r = (a²+b²) ⁄ 2b ,但始終找不到從弦矢算出弧長2s 的公式,也就是無法從a、b算出s。所以「弦矢求弧」也可以說是從弦矢求弧長的問題。而這個問題的本質,其實是「弧弦互算」,也就是在已知半徑的前提下從弧算出相對的弦長,反之就是從弦算出相對的弧長。
讀者如果稍微回憶一下以前曾經學過的公式,會想到我們還需要知道弧所對應的圓心角。這就是關鍵了,東方與西方文明的一個關鍵性的分岔點,發生在這個不起眼的小觀念――角。《九章》及之後的所有中國算書,都沒有討論到圓心角的問題――他們沒想到將弦與弧聯繫起來的關鍵是圓心角,當然也不曾想過要測量角了。因此缺乏角度概念的漢文明,始終無法解答「弧弦互算」的問題。筆者認為,「華人無角」這個歷史評論雖然有些過於簡化,卻大體上不失公允(延伸閱讀)。
以函數解答弧弦互算
所有圓彼此相似,給定圓心角後,伸縮半徑時只會使得角所對的弦和弧按比例放大或縮小(圖三);也就是說半徑在這個脈絡裡的角色就像比例常數,並不是問題的關鍵。因此,現代教科書大多令半徑為單位長,而本文也一律以「給定半徑r」為前提。
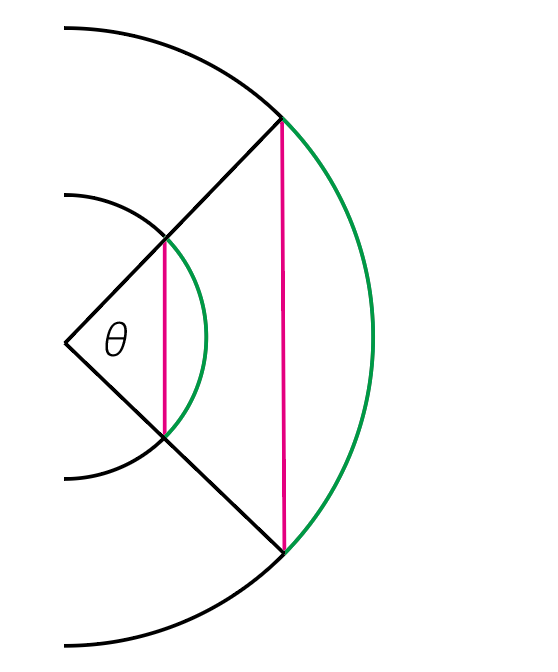
圖三|弦和弧的比例
(作者提供)
我們同時以θ表示圓心角,以及它的測量數值(角量)。因為圓具備任意旋轉的對稱性,所以θ所對的弧長/弦長只由角的大小決定,與角的方位無關。因此弧長/弦長全然由角量決定,這就是函數觀念:弧長/弦長是所對的圓心角的函數,在計算時分別會用arcθ和crdθ表示這兩個函數。小學用「度」(°)作為角量的單位,因此得到arcθ 的公式,也就是函數arc 的代數式為:arcθ= π ⁄ 180 ×rθ,定義域為0 ≦ θ ≦ 360。
到了高中改用「弳」作為角量的單位,因此換成另一條公式:arcθ = rθ,定義域為0 ≦ θ ≦ 2π。弧長公式是「反之亦然」的函數關係,意思是圓心角量決定它所對的弧長:s=arcθ,弧長也決定它所對的圓心角量:θ=arc⁻¹s。反算的公式為:θ =arc⁻¹s =180 ⁄ π× s ⁄ r度= s ⁄ r弳。
同樣地,若將角限定在0°~ 180°的範圍內,則角θ與弦c之間也有「反之亦然」的函數關係;圓心角量決定它所對的弦長:c = crdθ,弦長也決定它所對的圓心角量:θ = crd⁻¹c。
以圓心角為中介,arc和crd兩種函數可以實現「弧弦互算」,而配置如圖二的「弦矢求弧」也能算了:弧長2s = arc(crd⁻¹(2a)),題目中的矢長b用來決定半徑r。但問題是θ = crd⁻¹c 只是觀念上的函數,它並沒有代數表達式,也就是說它沒有「公式」,所以還是無法算出。其實歷史還有另一種可能,或許《九章》的作者群及後來的疇人曾思考過圓心角,但是苦於找不到θ = crd⁻¹c 的公式,因此只能停滯不前。
角度與天文曆法的關係
儘管如此,「缺了角」的漢文明仍然有高度的工程成就,不但建構出萬里長城,還打造了南北大運河,而這些工程在建設時都少不了大地測量。由此可見,大地測量並不一定需要角。《九章》的〈勾股〉章提供了足夠測量所需的數學。勾股就是直角三角形,《九章》從不討論它的銳角,只運用它的三邊比就足夠做大地測量了。西方文明使用一般三角形做測量的優點,是可以應用正弦定理與餘弦定理,但這兩個定理都是畢氏定理的推廣(〈勾股〉也有畢氏定理),所以有了角只是在計算上更方便一些,並沒有本質的差異。

▲ 缺了角的漢文明,仍然建構出萬里長城等需要大地測量的建設。
(Adobe Stock)
真正需要角度概念的是「弧弦互算」,它不但可以解決弦矢求弧問題,更是天文測量的基礎數學,可以說角的威力展現於量天(天文測量),而非量地(大地測量)。缺角對文明的損害,首先發生在天文與曆算。當19 世紀西方耶穌會的傳教士來到中國時,東方的曆算已經落後,西來會士靠著曆算本領進入欽天監,在朝廷裡找到了立足點。難道西方找到了「弧弦互算」的公式嗎?理論上並沒有,但實際上已經夠用,關鍵人物就是托勒密。
……【更多內容請閱讀科學月刊第657期】